filmov
tv
Finding tan(5) in terms of tan(19)
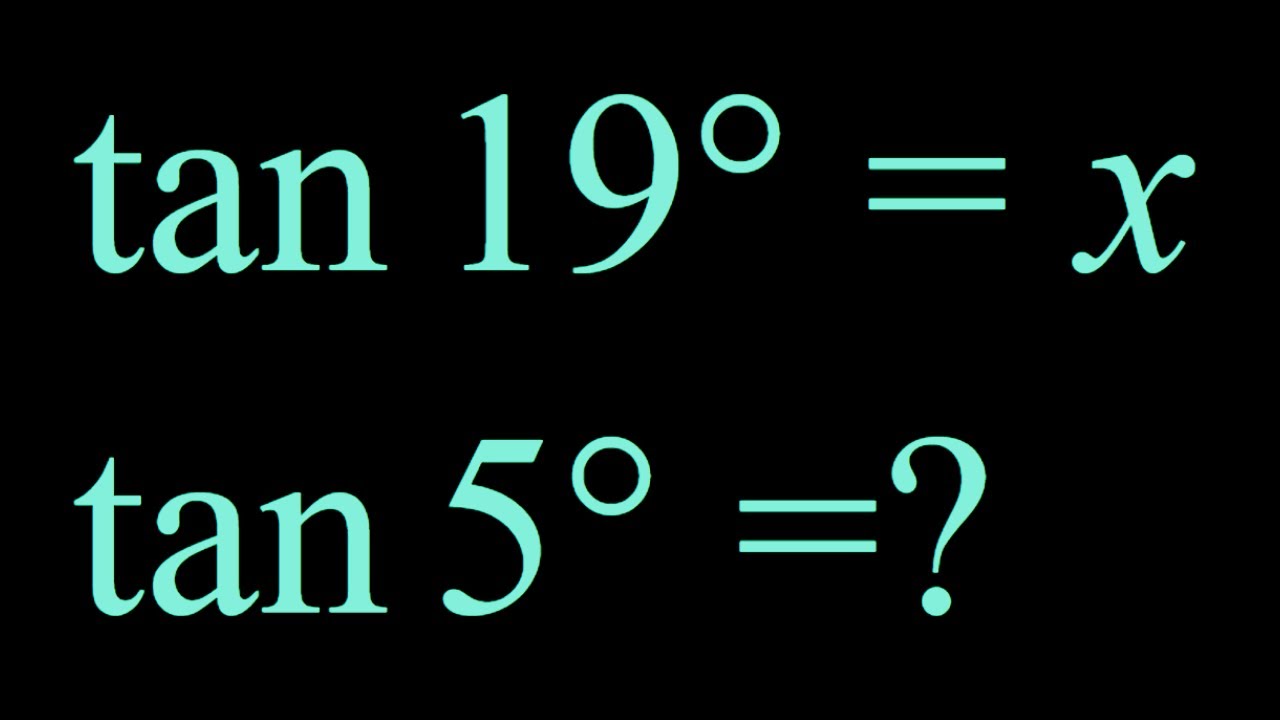
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #TrigonometricExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #TrigonometricExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
Finding tan(5) in terms of tan(19)
#Shorts Can you solve it? How to calculate tan 5 from tan 19?
Finding tanα if tan(α+β)=7 and tan(α-β)=5
If cot theta = 5/7, find tan theta
#Full Can you solve it? How to calculate tan 5 from tan 19?
How to find tan inverse using logtable
Evaluating tan(11°) in Terms of tan(17°)
Math 1316 Find tan(s+t) Using the Sum Identity for Tangent
Calculus 2 Exam Review Part6
Find Exact Value of Tan 195 Difference of Angles Q3
EXACT Value Of tan(5pi/12)
Find sin(x) if tan(x)+sec(x)=1.5
Evaluate the trig expression with inverse tan
Evaluating tan(14) in terms of tan(13)
Tan 19 Value
FIND THE VALUES OF TRIGONOMETRIC FUNCTIONS || TAN (19PI/3) || SIN(-11PI/3)
tan a = 1/5 and tan b = 1/239 Find tan(4a - b) IMPORTANT
Exact Value of tan(5pi/6) - Unit Circle Survival Guide
Finding the missing side by using Tan #maths #trigonometry #shorts
Given that tan 25°= a, express in terms of a . find tan 205°, Sin 25°, Cos 65° & Cos 245°
How to remove Sun Tan | How to remove Tanning | How to Detan | Dermatologist tips for Tanning
Find exact value for sin(sin^(-1)(-4/5) - tan^(-1)(3/4)). Sum and Difference Formula
find the value of tan5°tan25°tan30°tan65°tan85°#shorts
Relation b/w Trigonometrical functions | sin cos tan cot sec | #short | #shorts | #trigonometry
Комментарии
 0:09:07
0:09:07
 0:00:58
0:00:58
 0:12:37
0:12:37
 0:00:49
0:00:49
 0:04:31
0:04:31
 0:04:35
0:04:35
 0:00:55
0:00:55
 0:27:17
0:27:17
 5:47:36
5:47:36
 0:09:44
0:09:44
 0:10:35
0:10:35
 0:06:54
0:06:54
 0:03:56
0:03:56
 0:10:35
0:10:35
 0:00:05
0:00:05
 0:05:28
0:05:28
 0:05:52
0:05:52
 0:04:45
0:04:45
 0:00:29
0:00:29
 0:06:51
0:06:51
 0:00:19
0:00:19
 0:03:42
0:03:42
 0:00:58
0:00:58
 0:00:24
0:00:24