filmov
tv
Normal distribution's probability density function derived in 5min
Показать описание
The proof comes from Grossman, Stanley, I., Multivariable Calculus, Linear Algebra, and Differential Equations, 2nd., Academic Press, 1986., and Hamming, Richard, W. The Art of Probability for Engineers and Scientists, Addison-Wesley, 1991. This was summarized by Dan Teague of the North Carolina School of Science and Mathematics. This did not use characteristic functions or moment generating function to derive, because this explanation was straightforward. A disclaimer is that, in the second step, the improper integral appears without proper treatment that this is allowed. However, digging into the details of this would be beyond the scope for this video made to make the content simple.
Normal Distribution (PDF, CDF, PPF) in 3 Minutes
Probability Density Function of the Normal Distribution
Normal Distribution EXPLAINED with Examples
Probability Density Functions
Normal Distribution & Probability Problems
The Normal Distribution, Clearly Explained!!!
What is a Probability Density Function (pdf)? ('by far the best and easy to understand explanat...
Normal distribution's probability density function derived in 5min
30th Distinguished Statistician Colloquium: Dr. Nancy Reid's Lecture, 'When Likelihood Goe...
What is a Gaussian Distribution?
Density Curves and their Properties (5.1)
Why π is in the normal distribution (beyond integral tricks)
Probability density and mass functions
How normal probability distribution works
Explaining Probability Distributions
Probability Distribution Functions (PMF, PDF, CDF)
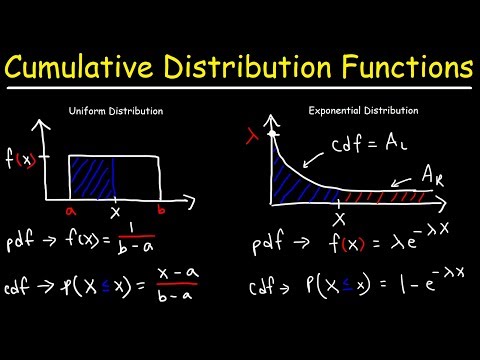
Cumulative Distribution Functions and Probability Density Functions
An Introduction to Continuous Probability Distributions
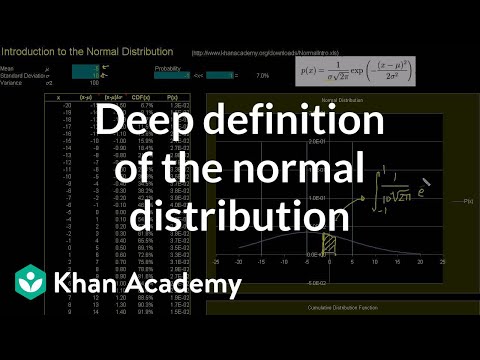
An Introduction to the Normal Distribution
Introduction to the normal distribution | Probability and Statistics | Khan Academy
Density Curves | Modeling data distributions | AP Statistics | Khan Academy
Standard Normal Distribution Tables, Z Scores, Probability & Empirical Rule - Stats
Normal Distribution: Probability Density Function Derivation
Tutorial 25- Probability Density function and CDF- EDA-Data Science
Комментарии
 0:05:26
0:05:26
 0:13:32
0:13:32
 0:10:59
0:10:59
 0:11:46
0:11:46
 0:29:30
0:29:30
 0:05:13
0:05:13
 0:09:46
0:09:46
 0:04:50
0:04:50
 1:11:41
1:11:41
 0:05:45
0:05:45
 0:09:37
0:09:37
 0:24:46
0:24:46
 0:06:56
0:06:56
 0:00:59
0:00:59
 0:12:54
0:12:54
 0:16:17
0:16:17
 0:11:02
0:11:02
 0:05:52
0:05:52
 0:05:27
0:05:27
 0:26:24
0:26:24
 0:09:34
0:09:34
 0:51:03
0:51:03
 0:23:31
0:23:31
 0:07:52
0:07:52