filmov
tv
What is a Stationary Random Process?

Показать описание
Explains the concept of stationarity in random processes, using an example and diagrams.
* Note that I unfortunately forgot to mention that Stationarity also requires that the joint distribution of X(t1) and X(t2) is the same as the joint distribution of X(t1+Δ) and X(t2+Δ), for any t1, any t2, and for all Δ. In summary, this means that the way in which X(t1) and X(t2) are related, is the same as the way in which X(t1+Δ) and X(t2+Δ) are related. In other words, the level of dependency between two values that are spaced Δ apart, doesn't change over time. Or from yet another perspective, how _independent_ they are from each other, doesn't change over time.
* If you would like to support me to make these videos, you can join the Channel Membership, by hitting the "Join" button below the video, and making a contribution to support the cost of a coffee a month. It would be very much appreciated.
Check out my search for signals in everyday life, by following my social media feeds:
.
* Note that I unfortunately forgot to mention that Stationarity also requires that the joint distribution of X(t1) and X(t2) is the same as the joint distribution of X(t1+Δ) and X(t2+Δ), for any t1, any t2, and for all Δ. In summary, this means that the way in which X(t1) and X(t2) are related, is the same as the way in which X(t1+Δ) and X(t2+Δ) are related. In other words, the level of dependency between two values that are spaced Δ apart, doesn't change over time. Or from yet another perspective, how _independent_ they are from each other, doesn't change over time.
* If you would like to support me to make these videos, you can join the Channel Membership, by hitting the "Join" button below the video, and making a contribution to support the cost of a coffee a month. It would be very much appreciated.
Check out my search for signals in everyday life, by following my social media feeds:
.
What is a Stationary Random Process?
STATIONARY RANDOM PROCESS::: First Order Stationary Processes
Strict-Sense Stationary Process and its Examples
Time Series Talk : Stationarity
The Supplies I Used in School
What does Wide Sense Stationary (WSS) mean?
Stationary & Non Stationary Process
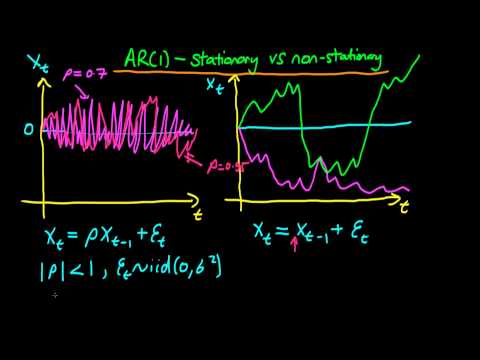
The qualitative difference between stationary and non-stationary AR(1)
Representation of Stationary Random Process
Are Stationary Random Processes Always Ergodic?
Stationary process
What are Stationary Random Processes? | Random Signal Processing |Random Processes|Signal Processing
Stationary Process | Strict Stationarity & Weak Stationarity || Time Series
Wide-Sense Stationary (WSS) Process and Examples
PTSP#Problem on Stationary Random Processes (SRP)#WSS RP
RP&LA|Unit 3|Random Processes|MA3355 | Stationary Process | Anna University Repeated 8 Mark Ques...
GEL7114 - Module 1.6 - Wide sense stationary (WSS) random processes
Stationary Random Processes | Digital Signal Processing # 13
Wide Sense Stationary Random Processes | Digital Signal Processing # 14
The Weirdest School Supplies
Making Starburst School Supplies #shorts
how I organize my stationery 🖊😙🌈✨ #shorts Natalies Outlet
Wide Sense Stationary Process
LECT-57: Correlation / Autocorrelation / Wide Sense Stationary Random Processs
Комментарии
 0:04:04
0:04:04
 0:07:53
0:07:53
 0:19:00
0:19:00
 0:10:02
0:10:02
 0:00:29
0:00:29
 0:06:23
0:06:23
 0:01:14
0:01:14
 0:07:57
0:07:57
 0:20:56
0:20:56
 0:04:55
0:04:55
 0:06:13
0:06:13
 0:20:45
0:20:45
 0:11:32
0:11:32
 0:19:15
0:19:15
 0:10:51
0:10:51
 0:25:24
0:25:24
 0:10:57
0:10:57
 0:21:30
0:21:30
 0:36:45
0:36:45
 0:00:28
0:00:28
 0:00:22
0:00:22
 0:00:21
0:00:21
 0:07:08
0:07:08
 0:10:26
0:10:26