filmov
tv
Enforcing the Unity of Space and Time Using Quaternions

Показать описание
Presented to the Fifth International Conference on the Ontology of Space-time in Albena, Bulgaria, May 2018. A view of number theory that can be applied broadly to physics.
Table ot contents
3:04 Zero, one, and the trivial group
10:00 Real numbers
13:56 Complex numbers
19:39 Space-time numbers
25:04 Simple math = physics
26:21 Special relativity & quaternion gravity
36:01 Purple Penguin derivation
48:00 Quaternion gravity and EM
50:55 Quaternion series QM
56:01 Testing quaternion series QM
59:45 Summary
Table ot contents
3:04 Zero, one, and the trivial group
10:00 Real numbers
13:56 Complex numbers
19:39 Space-time numbers
25:04 Simple math = physics
26:21 Special relativity & quaternion gravity
36:01 Purple Penguin derivation
48:00 Quaternion gravity and EM
50:55 Quaternion series QM
56:01 Testing quaternion series QM
59:45 Summary
Enforcing the Unity of Space and Time Using Quaternions
Enforcing the Unity of Space and Time Using Quaternions: 10' on Quaternion Series QM
Enforcing the Unity of Space and Time Using Quaternions: 25' on SR and gravity
Glow Stick Dance | #shorts
Using IMPROVED Animation Events in Unity
The Power of Teamwork - Teamwork Motivational Video
Enriched Finite Element Methods - Introduction to Partition of Unity methods
This is the ONLY game that got the KRISS Vector right...
FREE QUEST 2 GAME! FLY PLANES IN VR #vr #quest2 #oculusquest2
Phalanx: The Enforce Fighter A-144 (Unity 3D SHMUP 2/2) - 5120 x 1440 - Ultra Wide Gaming - 32:9
Why You Shouldn't Nest Your Code
Up or Down Party Game with Solo Cups! #youthministry #minutetowinit #crowdgames #partygames
Proteus Unity - Resilient, secure, through-rotor communications
Tim Nguyen vs Geometric Unity & Sentient Singularity Theory - Theory of Every0ne Live - 8.3.21
the unity drama continues (FULL VIDEO)
Camden City Spotlight: Unity Policing
Cary Unity Walk 2016 - Downtown Opening Remarks
Address To The United Nations by Emperor Haile Selassie
volleyball training Spike🏐🔥
NAMCOL JSC HISTORY: The Organisation of African Unity (4/5)
5 Steps to Fix Any Problem at Work | Anne Morriss | TED
Unite 2015 - Creating the Galaxy with Unity 5: Disruptor Beam on Star Trek Timelines
Lafayette law enforcement agencies and other groups hold 'Unity in the Community' event
[Unity 5] Object Pooling Tutorial
Комментарии
 1:00:27
1:00:27
 0:09:37
0:09:37
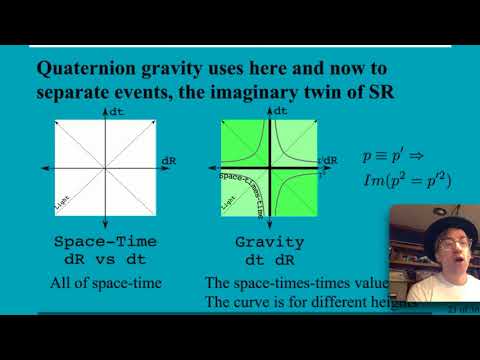 0:25:52
0:25:52
 0:00:16
0:00:16
 0:16:00
0:16:00
 0:05:59
0:05:59
 0:31:32
0:31:32
 0:00:47
0:00:47
 0:00:11
0:00:11
 0:01:30
0:01:30
 0:08:30
0:08:30
 0:00:16
0:00:16
 0:02:16
0:02:16
 3:34:54
3:34:54
 1:01:47
1:01:47
 0:01:33
0:01:33
 0:11:06
0:11:06
 0:28:10
0:28:10
 0:00:10
0:00:10
 0:14:44
0:14:44
 0:11:53
0:11:53
 0:49:38
0:49:38
 0:01:09
0:01:09
![[Unity 5] Object](https://i.ytimg.com/vi/LhqP3EghQ-Q/hqdefault.jpg) 0:20:56
0:20:56