Graph Data Structure 6. The A* Pathfinding Algorithm

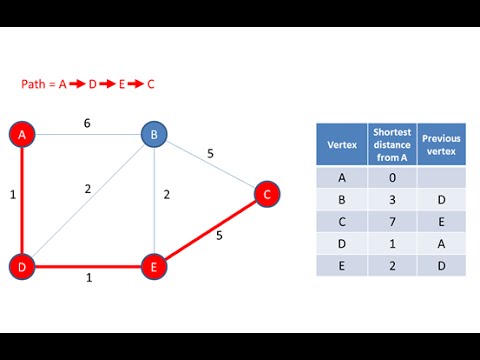
This is the sixth in a series of videos about the graph data structure. It includes a step by step walkthrough of the A* pathfinding algorithm (pronounced A Star) for a weighted, undirected graph. The A* pathfinding algorithm, and its numerous variations, is widely used in applications such as games programming, natural language processing, financial trading systems, town planning and even space exploration. This video demonstrates why the A* pathfinding algorithm may be more appropriate and more efficient than Dijkstra’s shortest path algorithm for many applications, because it is focussed on finding the shortest path between only two particular vertices. The video explains the need for an admissible heuristic, that is, a suitable estimate of the distance between each vertex in the graph and the destination vertex; the example shown here makes use of Manhattan distances for this purpose, calculated on the basis of the grid co-ordinates of each vertex. A description of the pseudocode that leads to an implementation of the A* pathfinding algorithm is also included.

When you watch this example, you will see there are occasions when the f values of some open vertices are the same, so the next current vertex is selected from these “for no particular reason”. As pointed out, making one choice or another could have a profound effect on the course of events that follow, but that very much depends on how the algorithm is implemented, and the anatomy of the graph being searched. The search described in this video concludes when the destination vertex is a neighbour of the current vertex - and it shares the lowest f value. Conceivably, another open vertex could have had a lower f value than the destination at this stage, so the search for a shorter path would continue. Again, exactly how the algorithm finishes is a matter of implementation. If you investigate this subject further, you will discover there are lots of ways the algorithm can be adapted. Using a priority queue for the open vertices is one way, pre-processing the graph data to calculate the h values is another. The basic A* pathfinding algorithm descried here is really just a starting point.

[ComputerScienceLessons]

Thanks to one of my viewers, Fro mik, for spotting an error in the pseudocode I included in my video about the A* pathfinding algorithm. The algorithm as I described it is correct. It points out the importance of calculating the f values of ALL the neighbours of the current vertex, including those neighbours that are already in the open list.

In my pseudocode, I add a neighbour of the current vertex to the open list if it’s not closed AND if it’s not already open. This is also a condition of calculating the f value, which is not correct. When vertex C is current, we need to recalculate the f value of vertex B, but my pseudocode would not do this because B is already open.
The pseudocode would work fine with the graph in my example, but if it was quicker to get from A to C via B, my pseudocode would not find the shortest path.

Below, you can see what the pseudocode should look like.

Needless to say, I will need to fix my VB.NET implementation code, which is based on my original pseudocode.
I you do spot any issues with any of my videos, do let me know and will try to put things right. I understand that even the smallest error can lead to big misunderstandings.

Please keep watching and keep sharing.

A*

Initialise open and closed lists
Make the start vertex current
Calculate heuristic distance of start vertex to destination (h)
Calculate f value for start vertex (f = g + h, where g = 0)
WHILE current vertex is not the destination
FOR each vertex adjacent to current
IF vertex not in closed list and not in open list THEN
Add vertex to open list
END IF
Calculate distance from start (g)
Calculate heuristic distance to destination (h)
Calculate f value (f = g + h)
IF new f value < existing f value or there is no existing f value THEN
Update f value
Set parent to be the current vertex
END IF
NEXT adjacent vertex
Add current vertex to closed list
Remove vertex with lowest f value from open list and make it current
END WHILE

[ComputerScienceLessons]

This is an updated version of the original video which corrects one of the g and f value calculations that was in error. I believe the calculations are all accurate now. I've added some additional comments to the description which you may find useful.

[potatocoder]

Thank you for this explanation! Its the most thorough one that I've come across :) Really appreciate people like you putting so much effort into providing quality education for free!

[jibran]

Your explanations are really very concise and clear! I was able to implement adjacency list, BFS, DFS and Dijkstra so far purely based on your videos and without even looking at the pseudo-code you provided! Now about to implement A*!

[nguyenluan]

Best explanation! Your narrative sounds like a BBC documentary haha

[cameronarnold]

Best explanation of A* I've found anywhere online! You're amazing :)

[trianglestudios]

No one gives an explanation like this. Works Finally.

[yuriyanisimov]

Thanks a lot for such an amazing explanation. Many other videos taking heuristic from thin air and not explaining the importance of it. This video on the other hand explains all pros and cons and edge cases if you choose the right heuristic value or wrong and what the outcome would be.

[MrChisnok]

You are doing amazing guides with your videos about Pathfinding, your explanation is always so clear. Thank You !

[paulmag]

Daniel, I am glad to see that you found yourself an interesting occupation after escaping from Alexander's castle and the Shadow.

[matthewevett]

A slight correction is needed to the end of the execution. The algorithm does not terminate when a goal node (P, in this case) is placed into Open, but only when that node is selected as the "current node". Thus, a goal node might be added to Open while there are still other nodes in Open with an equal or lower f-value. Those will need to be expanded before our goal node is finally selected for expansion, at which point the goal state will be detected and the algorithm will terminate.

[adis]

Agreed. Best explanation of A* so far on YouTube ;) Thank you!

[Hdrien]

Thank you so much for releasing such a well-made video. It is very clear and to the point. Loved it.

[justforfun]

Thank you so much for explaining this so clearly! Really appreciate that this is open source information!

[Ðogecoin]

Thank you so much for this explanation.

[redorchidee]

8:33 In another video on A* it was said the reason for choosing H over D in this case is that H happens to have a lower h value than D. Don't know if that applies here as well but it seems logical. Then at 10:18 the next current node would have to be K instead of J

[Adityakumar-ezud]

I'm happy, I got you! This was awesome

[eejain]

Very clear and detailed explanation, thank you!

[SombreroMan]

Correct me if I’m wrong, but in a nutshell, you just calculate the adjacent vertices distance to the current vertice you are on and the adjacent verticies distance from the destination. Then you travel the shortest option.

[auran_vesdranor]

Thank you for this great walkthrough!
You said "h()" is used for no particular reason if f has the same value. I think this is wrong. If f has the same value it makes sense to take the path that has the least distance to the goal (h) since it's more probable to lead faster to the goal node.