Graph Data Structure 4. Dijkstra’s Shortest Path Algorithm

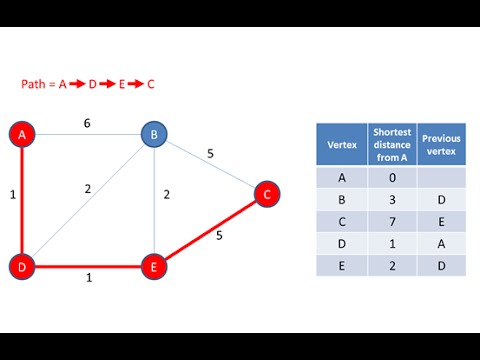
This is the fourth in a series of computer science videos about the graph data structure. This is an explanation of Dijkstra’s algorithm for finding the shortest path between one vertex in a graph and another. Indeed, this explains how Dijkstra’s shortest path algorithm generates a set of information that includes the shortest paths from a starting vertex and every other vertex in the graph. It also mentions why Dijkstra’s shortest path algorithm is an example of a greedy algorithm.

[daringdarius]

I don't know if you know this, and this is 4 years late, but this is one of the cleanest, easiest to understand video's (conceptually-wise) for Dijkstra's.


I've seen several, but this! This is the best one. :)

[assansanogo]

FINALLY SOME CLEAR STUFF. almost crying

[royazut]

!!!finally a good and simple explanation
oh tears of joy...
may the gods bless you with bugless codes

[adityapappu]

This is literally one of the cleanest, simplest, no-nonsense beautiful explanations of an algorithm I have ever watched on YouTube. Amazing. To-the-point. Crisp. And so easy to understand and digest. THANK YOU.

[SouravendraKrishnaDeb]

We won't be visiting A, again.
Me: CRIES LOUDLY

[faisalsal]

This video is your shortest path to learn Dijkstra Algorithm.

[reiniervanleeuwen]

This has to be the best explanation of Dijkstra's Shortest Path algorithm... Thanks a lot!

[TANEM]

You sir are BY FAR the BEST teacher of algorithms on YouTube or anywhere else I've seen algorithm lectures. THANK YOU FOR POSTING THIS! With your well-paced, methodical style you could probably teach anything!!!!

[ComputerScienceLessons]

Hi FTP
My scenario is for a non-directed graph (you can go backwards and forwards on any edge), so all the nodes can indeed be reached. However, for a directed graph, some nodes may be unreachable from the given start, as you have intimated. Dijkstra's algorithm finds the shortest paths only to the nodes that can be reached from the starting node. (if there is no path to a node from the start, it's irrelevant). The loop will end when all 'reachable' vertices have been visited. By the way, Dijkstra's algorithm doesn't work if the graph edges have negative weights.

[amine_fadssi]

The best video on the internet explaining the Dijkstra’s algorithm, thanks a lot sir.

[Jbbubanic]

I can't believe how well done this video was made. I appreciate your hard work at a visual representation of this algorithm.

[mikefriedman]

Absolutely the best explanation. Cleared up any and all lingering questions in my mind.

[matthewsattam]

Extremely clear, extremely well put together visually. Well done, and thank you.

[mikelanigan]

I must commend the quality and clarity of this video: it is by far the best video I've seen on YouTube to date on the subject of explaining Dijkstra's Algorithm. There are so many other videos that do not deal with the problem of keep a record of the shortest route sufficiently systematically enough, in my opinion. This video is systematic, showing the use of a table to perform the algorithm very clearly. Instruction of this level is not accidental; my congratulations to those involved in its production and execution. You have done the domain of Computer Science the world of good. Keep up the great work!

[lewistian]

BEST explanation of Dijkstra's algorithm EVER!

[taruchitgoyal]

I haven't found a better tutorial than this for understanding and computing distances using Dijkstra's algorithm. Thank you so much.

[Museko]

I'm watching a bunch of your videos to review for my Algorithms exam. Thanks a bunch for making these!

[johnstorm]

Even 6 years later, this is still the best explanation ever

[timuralmamedov]

Great explanation! Finally, I understood it. The table really helps to not get lost. Thank you so much!

[SpaceDisco]

It's really interesting, how sometimes one thorough example can clear up everything.