filmov
tv
Solving Schrodinger equation numerically pt 1

Показать описание
Part 1
An exact three-particle solver (but without relativstic effects). No basis functions. Instead discretization in 3D space using finite difference expressions is used. The eigenvalue and wavefunction is determined by using a fast and robust particle method. The corresponding Hamiltonian matrix often become nonsymmetrical due to mathematical transformations or nonsymmetrical finite difference expressions. This makes it troublesome for the conjugate gradient method which only deals with a symmetrical matrix and it also requires all eigenvalues to be positive. The particle method has no such restrictions (other than that the eigenvalues must be real).
An exact three-particle solver (but without relativstic effects). No basis functions. Instead discretization in 3D space using finite difference expressions is used. The eigenvalue and wavefunction is determined by using a fast and robust particle method. The corresponding Hamiltonian matrix often become nonsymmetrical due to mathematical transformations or nonsymmetrical finite difference expressions. This makes it troublesome for the conjugate gradient method which only deals with a symmetrical matrix and it also requires all eigenvalues to be positive. The particle method has no such restrictions (other than that the eigenvalues must be real).
Solving Schrodinger equation numerically pt 1
Solving Schrodinger equation numerically pt 2
Numerical solution of the 3D Schrodinger equation for the hydrogen atom
A PC app for solving the 2D Schrödinger equation for arbitrary infinite potential well
Solving the Schrodinger Equation 2/8: Hamiltonian
Numerical Solutions to Quantum Mechanics and Spectroscopy 5382 2021 Lecture
On the Numerical Solution of Two Dimensional Schrodinger Equation IJMR 61 1 12
XXI SBQT - A numerical-variational solution of the Schrödinger equation for H2+
Quantum Mechanics (UP): Numerical Solution To Schrodinger Equation and Minimum Uncertainty States.
Solutions to the Schrodinger Equation - Infinite Rectangular Potential (pt 1) | Quantum Mechanics
1D Quantum Gaussian Well | Numerical Solution to Schödinger Equation
Schrodinger equation solved numerically in 3D
Spherical Potential Solution (pt 2) - Radial Equation | Schrodinger | Quantum Mechanics
HOW TO APPLY SCHRODINGER EQUATION IN NUMERICAL|CSIR PREVIOUS YEAR QUESTION|QUANTUM MECHANICS LEC-08
Solving the Schrodinger Equation 3/8: Defining the Constants
Quantum potential well
Solving the Many-Electron Schrodinger Equation with Neural Networks
01 Quantum Harmonic Oscillator (Numerical solution)
Schroedinger Solver
The Time-Dependent Schrodinger Equation
Quantum tunneling animation (Python code in description)
Prerequisite Mathematical Knowledge for Solving Schrödinger's Equation for a Hydrogen Atom
Intro to Quantum Physics 1: Schroedinger Equation
Towards Closed-Form Solutions to the Few-Body Schrödinger Equation
Комментарии
 0:12:06
0:12:06
 0:11:35
0:11:35
 0:00:21
0:00:21
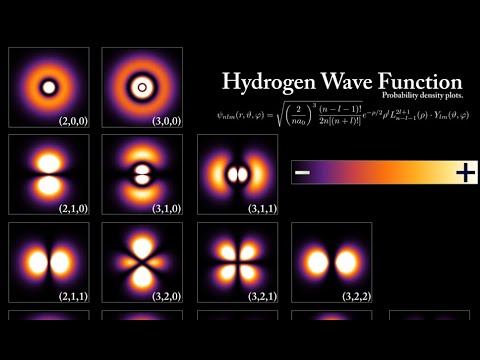 0:07:22
0:07:22
 0:02:48
0:02:48
 0:48:35
0:48:35
 0:01:03
0:01:03
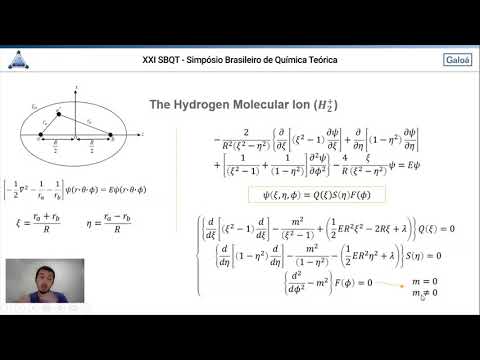 0:05:45
0:05:45
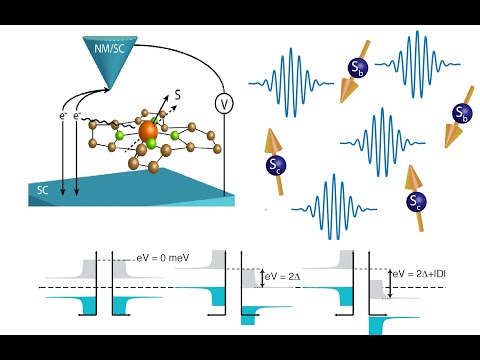 1:52:42
1:52:42
 0:25:36
0:25:36
 0:04:10
0:04:10
 0:00:34
0:00:34
 0:30:43
0:30:43
 0:21:14
0:21:14
 0:04:50
0:04:50
 0:00:09
0:00:09
 0:31:37
0:31:37
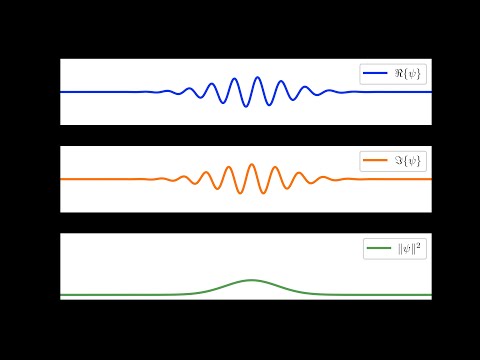 0:00:35
0:00:35
 0:04:00
0:04:00
 0:03:17
0:03:17
 0:00:26
0:00:26
 0:11:07
0:11:07
 0:13:50
0:13:50
 0:23:36
0:23:36