The Bolzano Weierstrass Theorem

preview_player
Показать описание
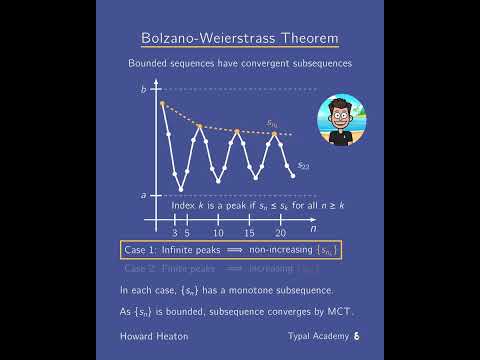
We prove the Bolzano-Weierstrass Theorem. This asserts that any bounded sequence of real numbers contains a convergent subsequence.

#mikedabkowski, #mikethemathematician, #profdabkowski, #realanalysis
  1. Mike, the Mathematician
  2. Bolzano-Weierstrass
  3. mike the mathematician
  4. mike dabkowski math
Рекомендации по теме
The Bolzano–Weierstrass theorem, 0:13:30

The Bolzano–Weierstrass theorem, a proof from real analysis

Short Proof of 0:05:21

Short Proof of Bolzano-Weierstrass Theorem for Sequences | Real Analysis

The Bolzano Weierstrass 0:07:44

The Bolzano Weierstrass Theorem

The Bolzano Weierstraß 0:05:48

The Bolzano Weierstraß Theorem

Proving Bolzano-Weierstrass with 0:16:18

Proving Bolzano-Weierstrass with Nested Interval Property | Real Analysis

Satz von Bolzano-Weierstrass 0:04:28

Satz von Bolzano-Weierstrass (EINFACH erklärt!)

3.3 Satz von 0:05:58

3.3 Satz von Bolzano-Weierstraß | Analysis für Anfänger: Folgen

Math 441 - 0:19:27

Math 441 - 2.5 Subsequences and the Bolzano-Weierstrass Theorem

[EM#17] Théorème de 0:08:55

[EM#17] Théorème de Bolzano-Weierstrass (Démonstration)

8.1 The Bolzano-Weierstrass 0:17:08

8.1 The Bolzano-Weierstrass Theorem

The Bolzano-Weierstrass Theorem 0:29:20

The Bolzano-Weierstrass Theorem - Real Analysis | Lecture 6

Lecture 20(C): Bounded 0:32:05

Lecture 20(C): Bounded Sequences: The Bolzano-Weierstrass Theorem

Prove every bounded 0:03:27

Prove every bounded sequence has a convergent subsequence (The Bolzano-Weierstrass Theorem)

Easiest Proof of 0:17:25

Easiest Proof of the Bolzano–Weierstrass Theorem

Real Analysis | 0:07:26

Real Analysis | Bolzano Weierstrass Theorem | Proof

The Bolzano-Weierstrass Theorem 0:10:42

The Bolzano-Weierstrass Theorem for Sequences

Bolzano Weierstrass Theorem 0:10:22

Bolzano Weierstrass Theorem for sequences by M. Arokiasamy

Bolzano-Weierstrass Theorem with 0:05:59

Bolzano-Weierstrass Theorem with solved example

MAT2125 - 3.5.3 0:02:59

MAT2125 - 3.5.3 - Bolzano-Weierstrass Theorem | Part 3 (02:58)

Bolzano Weierstrass Theorem 0:09:16

Bolzano Weierstrass Theorem | Every bounded sequence has a convergent sub sequence | Real sequence

Limit Point of 0:44:05

Limit Point of a Sequence, Bolzano-Weierstrass Theorem | B-W Theorem | Sequence of real numbers: 04

Visual Proof of 0:03:17

Visual Proof of the Bolzano Weierstrass Theorem

Bolzano–Weierstrass Theorem 0:01:27

Bolzano–Weierstrass Theorem

Bolzano Weierstrass Theorem 0:06:35

Bolzano Weierstrass Theorem | TRB Maths

Комментарии
Автор

I have attempted to understand the Bolzano-Weierstrass Theorem multiple times, but I was still confused until I watched your explanation. I am truly grateful for your video. Thank you so much!

Music-bbrw
Автор

The one that I learned at my uni was on the xy-plane.
I didn’t know that this theorem is also applied to 1 dimension.

akiraN
Автор

Do you have a proof of the nested interval property?

aubrey
Автор

Wow, are you writing everything in mirror-image?? great explanation

lucvansprang
Автор

So basically the theorem states that in a bounded sequence of real numbers, there must exist a converging subsequence? I saw another proof where a person just kept cutting the interval into halves and picking out a random a_n (the video from Zach Star). He kept talking about how the order is important. Could you perhaps explain that to me or make an example?

Brandonhuynh
Автор

I still don't understand why one of those intervals "must" contains infinitely many a_n
Is it obviously true or based on some statements ?

tungle
join shbcf.ru