filmov
tv
Prove the Logical Expression Tautology

Показать описание
Use the laws of logic to show that the following logical expression is a tautology without the truth table: Tautology Logic.
Please subscribe !
More videos on Logical Equivalence:
Play List of Logical Equivalence / Proposition Logic:
►Discrete Mathematics Workbooks:
Show less
Please subscribe !
More videos on Logical Equivalence:
Play List of Logical Equivalence / Proposition Logic:
►Discrete Mathematics Workbooks:
Show less
Proving a Tautology by Using Logical Equivalences
Prove the Logical Expression Tautology
Prove the Logical Expression Tautology
Propositional Logic − Logical Equivalences
Truth Table Tautology Logical Equivalence
17. Tautology by logical equivalences || Tautology without truth table || Discrete Mathematics
Proving a Tautology by Truth Table
Logical Equivalence Proof
Prove Logical Equivalence Using Laws
Proving a tautology
Tautology, Contradiction and Contingency - Logic - Discrete Mathematics
Logical Equivalence with out using truth table examples or equivalent formulas examples
Proof and Problem Solving - Logical Expression Simplification Example 02
7 - (Examples 6-7) Proving Logical Equivalence Using Laws
3 Ways to Show a Logical Equivalence | Ex: DeMorgan's Laws
Show that (p ∧ q) → (p ∨ q) is a tautology
Logical Equivalence of Two Statements
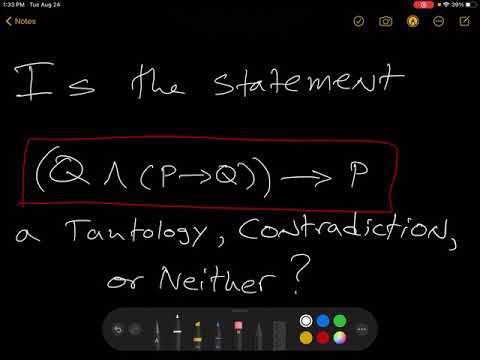
Tautology Contradiction Or Neither Example 1
Logical and tautological EQUIVALENCE ⟨05,02⟩
M1 V2 Logical Equivalencies
Tautology Contradiction Or Neither Example 2
Proving and Simplifying Propositions using Logical Equivalence Laws
Tautology, Contradiction, Contingency & Satisfiability
Show that p V ~p is a Tautology by using a Truth Table
Комментарии
 0:06:24
0:06:24
 0:06:40
0:06:40
 0:06:51
0:06:51
 0:17:23
0:17:23
 0:09:00
0:09:00
 0:14:24
0:14:24
 0:02:16
0:02:16
 0:13:12
0:13:12
 0:05:18
0:05:18
 0:03:39
0:03:39
 0:08:28
0:08:28
 0:16:23
0:16:23
 0:04:53
0:04:53
 0:05:59
0:05:59
 0:05:29
0:05:29
 0:03:11
0:03:11
 0:03:42
0:03:42
 0:05:38
0:05:38
 0:03:56
0:03:56
 0:26:12
0:26:12
 0:04:06
0:04:06
 0:07:37
0:07:37
 0:05:05
0:05:05
 0:02:07
0:02:07