filmov
tv
Math 4. Math for Economists. Lecture 05
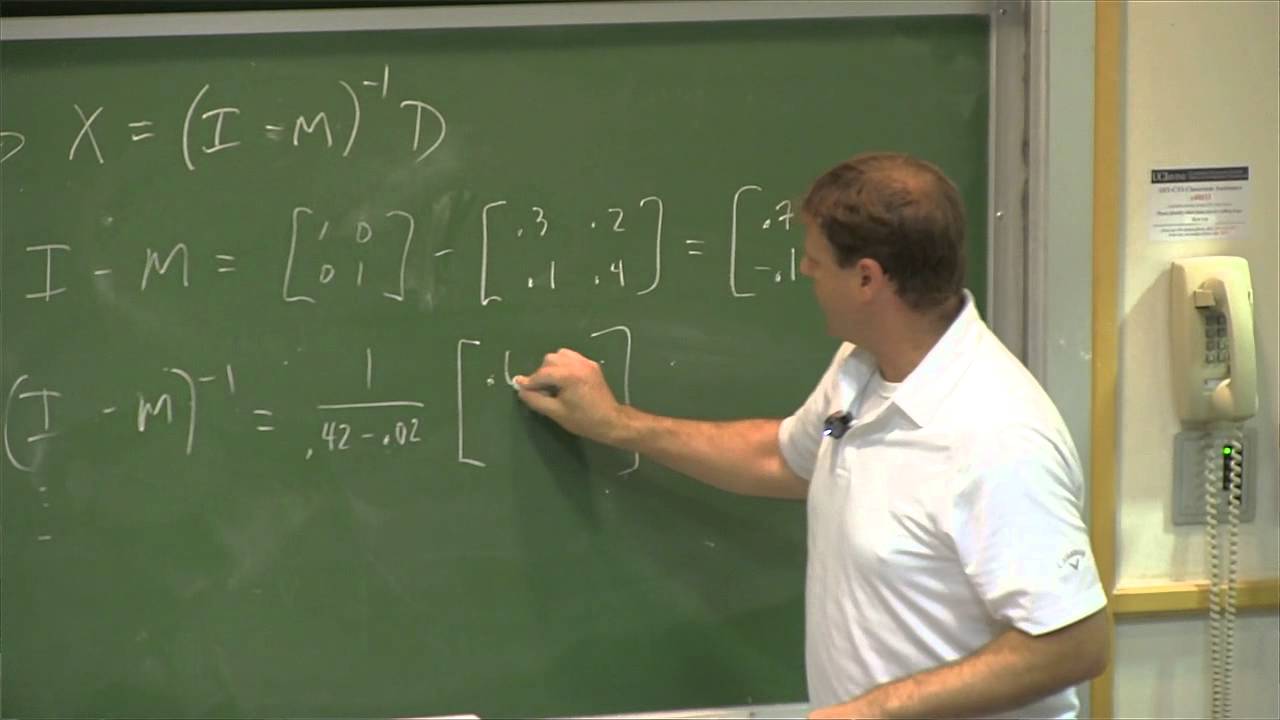
Показать описание
UCI Math 4: Math for Economists (Summer 2013)
Lec 05. Math for Economists
Instructor: Jason Kronewetter, Ph.D.
License: Creative Commons CC-BY-SA
Description: UCI Math 4 covers the following topics: linear algebra and multivariable differential calculus suitable for economic applications.
Recorded on August 14, 2013
Lec 05. Math for Economists
Instructor: Jason Kronewetter, Ph.D.
License: Creative Commons CC-BY-SA
Description: UCI Math 4 covers the following topics: linear algebra and multivariable differential calculus suitable for economic applications.
Recorded on August 14, 2013
Math 4. Math for Economists. Lecture 01. Introduction to the Course
Math 4. Math for Economists. Lecture 02
Math 4. Math for Economists. Lecture 04
Math 4. Math for Economists. Lecture 03
Math 4. Math for Economists. Lecture 13
Math 4. Math for Economists. Lecture 14
Math 4. Math for Economists. Lecture 12.
Math 4. Math for Economists. Lecture 10.
Math 4. Math for Economists. Lecture 08
Math 4. Math for Economists. Lecture 15: Final Review
Math 4. Math for Economists. Lecture 05
Math 4. Math for Economists. Lecture 09
Mathematics for Economists
Math 4. Math for Economists. Lecture 07.
Math 4. Math for Economists. Lecture 06
Math 4. Math for Economists. Lecture 11.
Mathematics for Economics - I
MATHS TOPICS WITHIN AN ECONOMICS DEGREE | Maths with Meg
Eric Weinstein: What Math and Physics Can Do for New Economic Thinking
John Kay: People, Not Iron Ore: The Limits of Math in Economics (4/5)
Math for Economists Week 3-4: Computation of Determinants
A Creative Philosophy for Mathematical Economics
Fundamental Method Of Mathematical Economics by Alpha Chiang BUY NOW: www.PreBooks.in #viral #shorts
Textbooks for Mathematical Economics
Комментарии
 1:42:01
1:42:01
 1:20:00
1:20:00
 1:45:11
1:45:11
 1:46:53
1:46:53
 1:31:32
1:31:32
 1:40:19
1:40:19
 1:15:01
1:15:01
 1:26:12
1:26:12
 1:40:43
1:40:43
 1:35:45
1:35:45
 1:46:36
1:46:36
 0:34:07
0:34:07
 0:08:36
0:08:36
 1:46:46
1:46:46
 1:44:00
1:44:00
 1:42:22
1:42:22
 0:00:13
0:00:13
 0:05:48
0:05:48
 0:19:07
0:19:07
 0:02:58
0:02:58
 0:21:53
0:21:53
 0:21:41
0:21:41
 0:00:16
0:00:16
 0:16:00
0:16:00