filmov
tv
Feynman would be proud
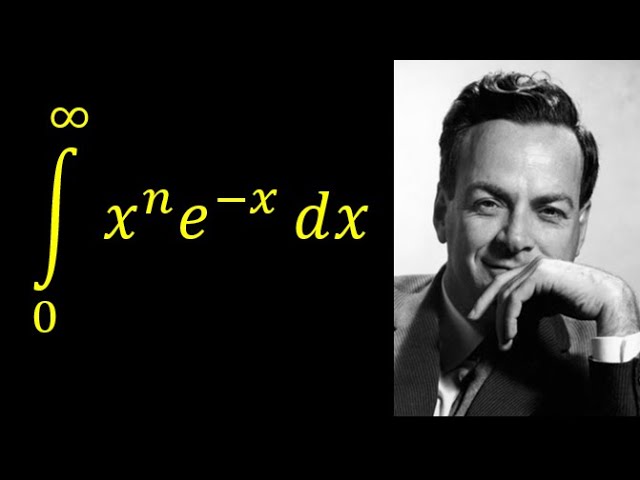
Показать описание
Feynman would be proud
We calculate the integral x^n exp(-x) from 0 to infinity using Feynman's technique. This is a must see for all the calculus students out there, enjoy!
We calculate the integral x^n exp(-x) from 0 to infinity using Feynman's technique. This is a must see for all the calculus students out there, enjoy!
Feynman would be proud. A Wonderful Generalized Integral.
Feynman would be proud
Feynman’s Technique Is The MOST Overpowered Integration Technique EVER Existed!
The Feynman Technique, Study Tips From a Professor That Wants You To Learn Faster, Better, Smarter
Great Minds: Richard Feynman - The Uncertainty Of Knowledge
Great Quote - Feynman on the Power of Education
THE FEYNMAN SERIES - Honours
How to make your asian parents proud
Richard Feynman Life Lesson
The Beauty of Mathematics #inspiration #themanwhoknewinfinity
Gauss would be Proud.
BBC - The Fantastic Mr Feynman
Richard Feynman Life Lesson on Study
The Best Teacher We've Never Had Richard Feynman
How To Study Physics Using The Feynman Technique
Richard Feynman Life Lesson | Richard Feynman Quotes | Feynman Quotes | Richard Feynman Motivation
Richard Feynman!
'Are you an ATHEIST?'- Mehdi Hasan asks Prof. Richard Dawkins #shorts #atheism #religion
Weekend Update: JoJo Siwa on Gay Pop and Her Bad Girl Era - SNL
Janitor Richard Goodall Sings An Unforgettable Cover Of 'Faithfully' By Journey | Finals |...
Waffle House - SNL
SURELY YOU'RE JOKiNG MR. FEYNMAN #richardfeynman
100 MOTIVATIONAL QUOTES OF RICHARD FEYNMAN | MOTIVATIONAL VIDEO
The Secret to Learning Things Faster with the Feynman Technique
Комментарии
 0:13:55
0:13:55
 0:03:44
0:03:44
 0:03:06
0:03:06
 0:12:44
0:12:44
 0:02:51
0:02:51
 0:01:51
0:01:51
 0:03:57
0:03:57
 0:00:06
0:00:06
 0:00:14
0:00:14
 0:00:59
0:00:59
 0:12:07
0:12:07
 0:59:37
0:59:37
 0:00:10
0:00:10
 0:00:36
0:00:36
 0:02:13
0:02:13
 0:00:23
0:00:23
 0:11:06
0:11:06
 0:00:35
0:00:35
 0:03:28
0:03:28
 0:05:05
0:05:05
 0:03:39
0:03:39
 0:00:05
0:00:05
 0:07:10
0:07:10
 0:06:11
0:06:11