filmov
tv
Measurement Problem in Quantum Mechanics

Показать описание
The measurement problem
Other places you can find content from me:
Patreon - authortomharper
Blog - The Cynical Philosopher
Twitter - @AuthorTomHarper
Amazon - Author Profile
My science fiction series available on Amazon
Incarnate: Existence
Incarnate: Essence
Incarnate: Schism
Other places you can find content from me:
Patreon - authortomharper
Blog - The Cynical Philosopher
Twitter - @AuthorTomHarper
Amazon - Author Profile
My science fiction series available on Amazon
Incarnate: Existence
Incarnate: Essence
Incarnate: Schism
The Problem with Quantum Measurement
The measurement problem in quantum mechanics with physicist Sean Carroll and Joe Rogan
What is the quantum measurement problem?
'The measurement problem violates the Schrödinger equation' | Roger Penrose on #quantummec...
Sean Carroll explains: what is the measurement problem in quantum mechanics?
The Measurement Problem in Quantum Mechanics: A Discussion of Interpretations and Experiments
David Albert: The Measurement Problem of Quantum Mechanics
Measurement Problem in Quantum Mechanics #physics
John Martinis: Quantum Systems Engineering
What’s the measurement problem in quantum mechanics?
Chaos: The real problem with quantum mechanics
What is the Measurement Problem of Quantum Mechanics? | David Albert
Part 1: Solution To The Measurement Problem
Why Quantum Mechanics Is an Inconsistent Theory | Roger Penrose & Jordan Peterson
Quantum Interactions and the Measurement Problem - Joe Rogan #shorts #joerogan #jre
The Measurement Problem in Quantum Physics: Reality vs. Observation!
Understanding Quantum Mechanics #5: Decoherence
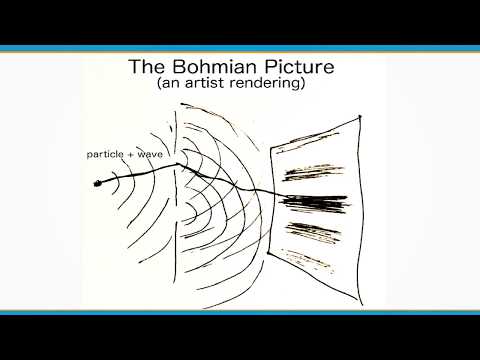
The Measurement Problem in Quantum Mechanics & Bohmian Mechanics
What is Quantum Mechanics Really Trying to Tell us about Reality? Featuring @SabineHossenfelder
Measurement Problem in Quantum Mechanics
the measurement problem of quantum mechanics
Unbelievable Truth About Quantum Mechanics Measurement Problem Uncovered #watchwhenbored #shorts
Sean Carroll on the Measurement Problem and Quantum Field Theory
Joe Rogan on what is Quantum Measurement #joerogan #podcast
Комментарии
 0:06:57
0:06:57
 0:01:00
0:01:00
 0:00:44
0:00:44
 0:01:00
0:01:00
 0:02:54
0:02:54
 0:08:49
0:08:49
 2:03:14
2:03:14
 0:01:00
0:01:00
 0:58:56
0:58:56
 0:00:57
0:00:57
 0:11:44
0:11:44
 0:11:08
0:11:08
 0:27:28
0:27:28
 0:06:34
0:06:34
 0:00:48
0:00:48
 0:00:49
0:00:49
 0:12:32
0:12:32
 0:05:46
0:05:46
 0:19:49
0:19:49
 0:04:42
0:04:42
 0:00:28
0:00:28
 0:00:57
0:00:57
 0:02:02
0:02:02
 0:00:14
0:00:14