filmov
tv
The Measurement Problem in Quantum Mechanics & Bohmian Mechanics

Показать описание
A brief description of the measurement problem in traditional quantum mechanics, and why Bohmian mechanics does not have the same issues.
P.S. I realize that I slightly misread the quote by Wheeler. Oops.
P.S. I realize that I slightly misread the quote by Wheeler. Oops.
The Problem with Quantum Measurement
What is the quantum measurement problem?
Sean Carroll explains: what is the measurement problem in quantum mechanics?
David Albert: The Measurement Problem of Quantum Mechanics
The Measurement Problem in Quantum Mechanics: A Discussion of Interpretations and Experiments
The measurement problem in quantum mechanics with physicist Sean Carroll and Joe Rogan
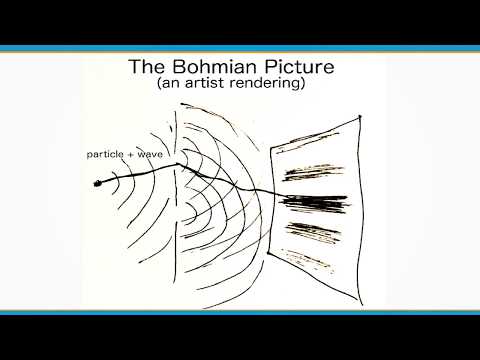
The Measurement Problem in Quantum Mechanics & Bohmian Mechanics
Part 1: Solution To The Measurement Problem
Quantum Consciousness Explained | How the Brain’s Quantum Processes Could Unlock Parallel Universes?...
The Measurement Problem in Quantum Physics: Reality vs. Observation!
Why Quantum Mechanics Is an Inconsistent Theory | Roger Penrose & Jordan Peterson
Measurement Problem in Quantum Mechanics #physics
David Albert & Tim Maudlin: The Measurement Problem, Solved?
Episode 36: David Albert on Quantum Measurement and the Problems with Many-Worlds
What’s the measurement problem in quantum mechanics?
What is the Measurement Problem of Quantum Mechanics? | David Albert
Chaos: The real problem with quantum mechanics
Understanding Quantum Mechanics #5: Decoherence
Measurement Problem in Quantum Mechanics
The Truth About Quantum Physics: Why the Measurement Problem Is Misunderstood
How Does the Measurement Problem Impact Quantum Mechanics?
'The measurement problem violates the Schrödinger equation' | Roger Penrose on #quantummec...
The Measurement Problem In Quantum Mechanics Explained!
Decoding the Quantum Enigma: The Measurement Problem Explained
Комментарии
 0:06:57
0:06:57
 0:00:44
0:00:44
 0:02:54
0:02:54
 2:03:14
2:03:14
 0:08:49
0:08:49
 0:01:00
0:01:00
 0:05:46
0:05:46
 0:27:28
0:27:28
 0:06:10
0:06:10
 0:00:49
0:00:49
 0:06:34
0:06:34
 0:01:00
0:01:00
 0:05:32
0:05:32
 1:42:34
1:42:34
 0:00:57
0:00:57
 0:11:08
0:11:08
 0:11:44
0:11:44
 0:12:32
0:12:32
 0:04:42
0:04:42
 0:05:59
0:05:59
 0:00:44
0:00:44
 0:01:00
0:01:00
 0:06:02
0:06:02
 0:06:50
0:06:50