filmov
tv
What is the Intersection of the Null Set? (Set Theory Proof)

Показать описание
A video looking proving that the intersection of the null set is the universal class: V=⋂∅.
This series covers the basics of set theory and higher order logic. In this month we are looking at the Operations and Relations of Sets. This month includes unions, intersections, differences, power sets, Cartesian products, functions, ordered pairs and more! We are also looking at the fifth and sixth axioms of a basic universe, following Neumann Berneays Gödel (NBG) set theory. In the next month we will look at Peano Arithmetic. (#SetTheory #Logic)
Sponsors: Joshua Furman, Joshua Opell, NBA_Ruby, Eugene SY, Antoinemp1, Antibody, Ismail Fagundes, Adrien Ecoffet, Tom Amedro, Christopher McGevna, Joao Sa, and Dennis Sexton. Thanks for your support!
Information for this video gathered from The Stanford Encyclopedia of Philosophy, The Internet Encyclopedia of Philosophy, The Cambridge Dictionary of Philosophy, The Oxford Dictionary of Philosophy and more!
This series covers the basics of set theory and higher order logic. In this month we are looking at the Operations and Relations of Sets. This month includes unions, intersections, differences, power sets, Cartesian products, functions, ordered pairs and more! We are also looking at the fifth and sixth axioms of a basic universe, following Neumann Berneays Gödel (NBG) set theory. In the next month we will look at Peano Arithmetic. (#SetTheory #Logic)
Sponsors: Joshua Furman, Joshua Opell, NBA_Ruby, Eugene SY, Antoinemp1, Antibody, Ismail Fagundes, Adrien Ecoffet, Tom Amedro, Christopher McGevna, Joao Sa, and Dennis Sexton. Thanks for your support!
Information for this video gathered from The Stanford Encyclopedia of Philosophy, The Internet Encyclopedia of Philosophy, The Cambridge Dictionary of Philosophy, The Oxford Dictionary of Philosophy and more!
What is the Intersection of a Set? (⋂A)
Intersection of Sets, Union of Sets and Venn Diagrams
What is the Intersection of Two Sets? (A⋂B)
The Intersection of Two Sets
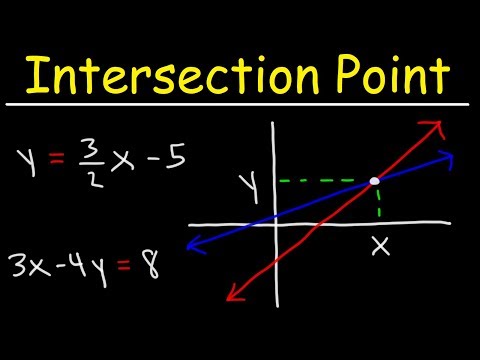
Finding The Point of Intersection of Two Linear Equations With & Without Graphing
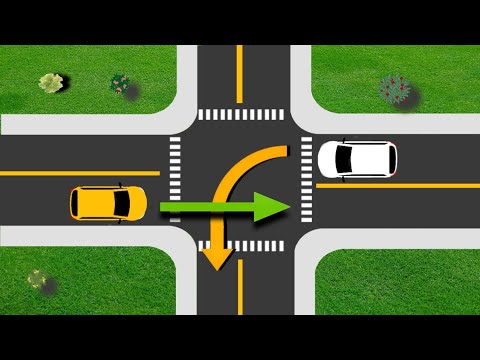
Which Car Should Pass The Intersection First | Right of Way Rule | Driving tips.
Intersection of Sets
The Intersection of Science and Meaning | Dr. Brian Greene | EP 486
Intersection of Two circles | Lecture- 4 | Circles | Math | Grade 11 | JEE
Venn Diagrams (A intersection B, A' union B')
What term is used to describe the intersection of decentralized finance and blockchain-based gaming?
The Intersection of Science and Religion with Neil deGrasse Tyson
The Intersection of War and Climate Change | Victor Ochen | TED
How to Find the Intersection of Two Sets with Numbers Short Video
What Is the Intersection of AI and Blockchain?
How to find the intersection point of two linear equations
❖ Sets, Union and Intersection of Two Sets ❖
Finding the Intersection of Two Lines
Math is the intersection of art and science | Ali Rahman | TEDxYouth@Columbus
What is the Intersection of the Null Set? (Set Theory Proof)
Finding the intersection of two lines without graphing
Union and intersection of set
Ex 1: Find the Intersection of Two Linear Functions (Integer Coordinates)
What is The Intersection Theorem? (Set Theory Proof)
Комментарии
 0:07:16
0:07:16
 0:11:49
0:11:49
 0:05:55
0:05:55
 0:05:47
0:05:47
 0:05:23
0:05:23
 0:01:51
0:01:51
 0:02:29
0:02:29
 1:33:29
1:33:29
 0:23:39
0:23:39
 0:00:37
0:00:37
 0:01:06
0:01:06
 0:51:51
0:51:51
 0:11:27
0:11:27
 0:00:28
0:00:28
 0:05:56
0:05:56
 0:04:01
0:04:01
 0:05:40
0:05:40
 0:06:58
0:06:58
 0:07:34
0:07:34
 0:07:20
0:07:20
 0:08:16
0:08:16
 0:01:01
0:01:01
 0:04:15
0:04:15
 0:10:58
0:10:58