filmov
tv
Relativistic Momentum- Correction to Newton's second law

Показать описание
The momentum p of an object of mass m traveling with a velocity v is given by mv. This equation for momentum is a classical or Newtonian one and gives rise to Newton's second law also known as the force law where force is the product of mass and acceleration of a body. But with Einstein's theory of relativity, these equations for momentum and force do not hold well at relativistic speeds. Special relativity forces us to make corrections to the ideas of momentum and force thereby resulting in a correction to Newton's second law. The video introduces the idea of relativistic momentum and goes on to derive the expression for relativistic momentum using the conventional collision problem from the points of view of two different inertial frames of reference in relative motion. The resulting correction term to Newton's second law is also derived. The video forms part of a series of videos on Special Relativity that are being posted on this channel.
Relativistic Momentum- Correction to Newton's second law
Is relativistic mass real?
Time Dilation - Einstein's Theory Of Relativity Explained!
Week 8-6 Relativistic Linear Momentum
Lecture 56: Conservation of Energy and Momentum in Special Relativity
Lecture 6 Acceleration and Forces in Relativity The Birth of Fields
Lecture 5 Part 1 Relativistic Energy and Momentum
Is Newtonian momentum conserved? | Special Relativity | meriSTEM
155 Special Relativity Momentum
22.3: Relativity-Invariants, Momentum, and Energy
Newton's 2nd Law with Special Relativity
Our Ignorance About Gravity
Relativistic Force
Relativistic expression of mass
Derivation of Relativistic Momentum
Relativistic energy and Minkowski space (ASGv2Ch32Lect03)
Modern Physics, Lecture 12: Relativistic Kinematics. Energy and Momentum.
Four-Vectors in special relativity
Lecture 2: Kinematics in special relativity, Doppler effect
Relativistic corrections to atomic spectra
Introduction to Relativistic Momentum and Energy
Special Relativity Lec 11 Part 3
PoNing Chen | Angular momentum in general relativity
Newtons Second Law , Relativistic Energy Momentum || Relativistic Mechanics || Lecture 16
Комментарии
 0:22:18
0:22:18
 0:09:02
0:09:02
 0:08:06
0:08:06
 0:08:34
0:08:34
 0:23:45
0:23:45
 0:31:09
0:31:09
 0:37:09
0:37:09
 0:06:54
0:06:54
 0:10:18
0:10:18
 0:57:02
0:57:02
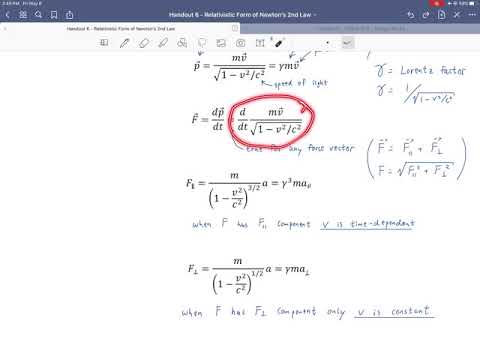 0:32:54
0:32:54
 0:05:38
0:05:38
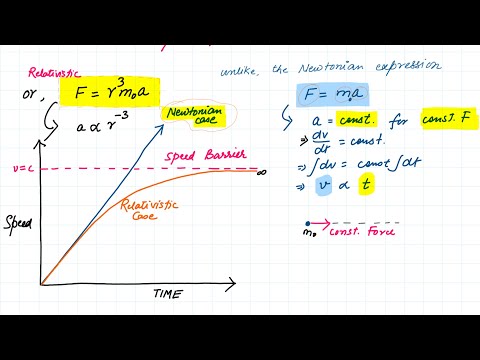 0:19:37
0:19:37
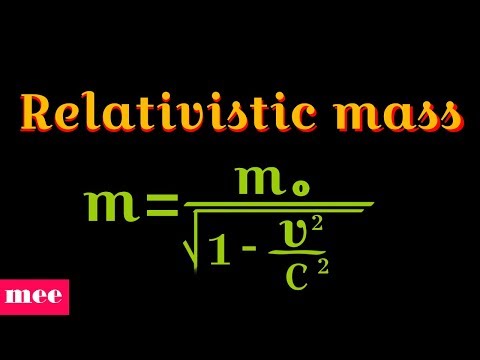 0:13:43
0:13:43
 0:15:26
0:15:26
 0:12:57
0:12:57
 0:48:23
0:48:23
 1:29:40
1:29:40
 1:37:29
1:37:29
 1:09:27
1:09:27
 1:04:19
1:04:19
 0:30:08
0:30:08
 0:46:25
0:46:25
 0:33:51
0:33:51