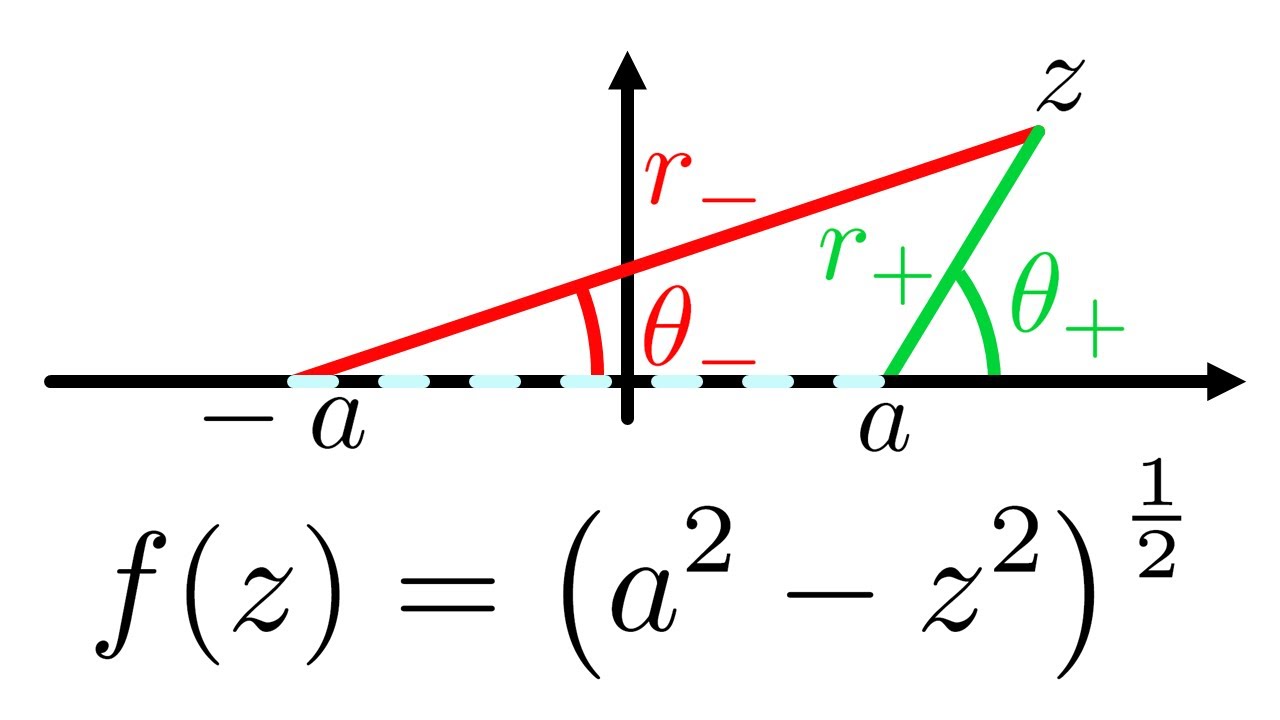
Understanding branch cuts: f(z) = (a²-z²)^½

preview_player
Показать описание
Gaining some understanding and intuition about branch points and branch cuts, taking as an example the function f(z) = (a²-z²)^½. We discuss how branch cuts can be used to make f(z) single-valued and show how making a branch cut is equivalent to restricting the arguments of z relative to the function's branch points. Next time we'll use these results to help evaluate a certain contour integral!

About me: I studied Physics at the University of Cambridge, then stayed on to get a PhD in Astronomy. During my PhD, I also spent four years teaching Physics undergraduates at the university. Now, I'm working as a private tutor, teaching Physics & Maths up to A Level standard.

#mathematics #complexnumbers #branchpoints #branchcuts #exponential #complexanalysis #fractionalpowers #multivalued #argument #modulus #argganddiagram #maths #math #science #education
  1. Dr Ben Yelverton
Рекомендации по теме
Understanding branch cuts: 0:21:36

Understanding branch cuts: f(z) = (a²-z²)^½

Introducing Branch Points 0:09:30

Introducing Branch Points and Branch Cuts | Complex Variables

(PCb22) Intro. to 0:35:54

(PCb22) Intro. to Branch Cuts and Branch Points

EX: Branch cut 0:10:43

EX: Branch cut of the product of two square roots

Branch points and 0:06:16

Branch points and a branch cut for the complex logarithm

Complex Analysis 17 1:15:00

Complex Analysis 17 - Branch, Branch points and Branch cuts of a Multi Valued Function

Branch Points and 0:09:26

Branch Points and Branch Cuts

complex analysis: polar 0:13:53

complex analysis: polar forms and how branch cuts work

A little app 0:07:16

A little app to see the branch cuts of functions

A contour integral 0:17:53

A contour integral around a branch point

A contour integral 0:03:58

A contour integral and a branch cut

Branch Point and 0:45:03

Branch Point and Branch Cut |Multi valued Functions in Complex Analysis|Part 1|Theta Classes

Branch cut of 0:15:45

Branch cut of Log functions || Complex Analysis

Complex Analysis: Logarithms 0:34:55

Complex Analysis: Logarithms and Branch Cuts

Complex Workshop - 0:16:13

Complex Workshop - Riemann surfaces and branch cuts (chalkboard test video)

Branch points and 0:14:30

Branch points and branch cuts

What do complex 0:28:33

What do complex functions look like? | Essence of complex analysis #4

[CA/Week 4] 3. 0:11:36

[CA/Week 4] 3. Extraction of the regular branch of the power type function [example]

1.5 Branch cuts 0:15:02

1.5 Branch cuts

[CA/Week 4] 6. 0:06:17

[CA/Week 4] 6. Practice with regular branches II.

[CA/Week 4] 9. 0:10:56

[CA/Week 4] 9. Practice with regular branches V.

Complex Analysis: Fancy 0:48:28

Complex Analysis: Fancy Branch Cuts

1.5 Branch cuts 0:13:27

1.5 Branch cuts (cont.)

Branch of log(z) 0:01:01

Branch of log(z)

Комментарии
Автор

Finally...something regarding complex analysis...love the video....I would greatly appreciate it if you would make more videos on this topic...especially branch cuts of more complicated functions....

DihinAmarasigha-uphf