Complex Analysis: Fancy Branch Cuts

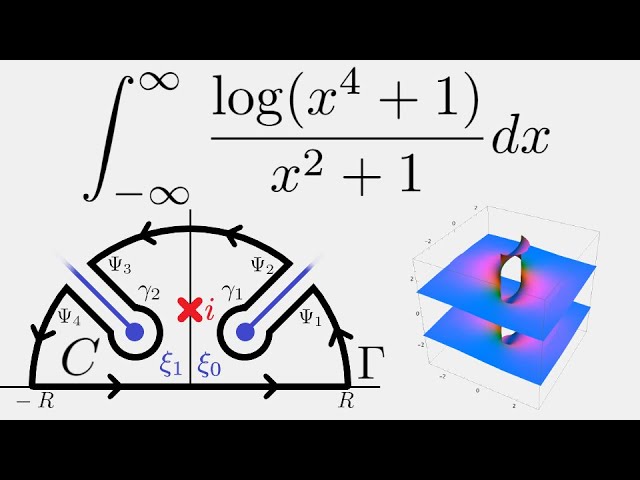
Today, we evaluate the integral of log(x^4+1)/(x^2+1) from -infinity to infinity using contour integration.

[girianshiido]

Saying that a logarithm of a product of complex numbers is the sum of the logarithms of its factors is of course incorrect. It is true in some cases but it’s not true in general. This is one of the difficulty of dealing with logarithms of complex numbers. The chosen branch cut of log(z^4+1) is not equal to the natural logarithm of z^4+1 when z is real (you have +8iπ). The arguments have to be chosen carefully in order to cancel themselves.

[manstuckinabox]

I love how intimidating 6:23 the product sign is, they're like these "I'm a tough guy" mini people you can easly destroy with a log. (in both cases ;p).

[karomusaelyan]

Hello can you slove this integeal 0to infinity ln(x²+1)/(x²+1)

[trannam]

In 20:14 how to know which side of omega should we approach for each psi? Why psi 1 need to spin around whereas psi was just approach directly?

[kummer]

A 3 dimensional picture of this surface illustrates WHY such multi branched functions requires SUCH contour.
Contouring these functions is the main task because it reveals the nature of such multi branch functions that cuts with itself or surfaces that clip with each other.

Would be great if we could have 3D images of what is going on through the process of integration. I know that such videos are intended to be aimed at scholars with the intention of finding the Riemann sum or a closed form of such sum. But there's a lot of more happening when such contour is decided in that way around the POLES.

For me this is my daily morning. Classical complex integration IS a theme on itself. There should be an ENTIRE book dedicated only to this fascinating topic.

[Carnifindion]

ξ is pronounced like 'hexi' but without the 'he'

[lordstevenson]

When your evaluating integrals over separate curves Γ, ψ1, ψ2. Is there a common way of knowing which integrals contribute 0, before computing them, is this intuition or a theorem or just knowing beforehand?

[Pyroguy]

everybody...lol im trained to hear that every time I click on one of your videos. I'm doing my phd in physics right now and I want to thank you so much for all your help on complex analysis. By far, this channel has been the reason I've been able to handle a lot of the mathematical physics problems they throw at me on exams...

[lordstevenson]

Starting the holidays with a juicy integral.

This is a throw away thought, since I haven’t done a complex analysis course my knowledge is based on random videos, after seeing this example it’s made me think.

My question is, are branch cuts only linear intervals or could they be polynomial or some other function? Like a function not being defined along some nonlinear branch cut.

[taterpun]

You can also solve this with real analysis (I just realized this was not the integral, but hopefully still a cool solution)

I = (-∞, ∞)∫log(x^4 + 1)/x^2dx

= 2(0, ∞)∫log((x^2 + 1)x^2)/x^2dx

= 2(0, ∞)∫log(x^2 + 1/x^2)/x^2dx + 2(0, ∞)∫log(x^2 )/x^2dx

= 2(0, ∞)∫log(x^2 + 1/x^2)/x^2dx - 2(0, ∞)∫log(1/x^2 )/x^2dx

define I(t) = 2(0, ∞)∫log(tx^2 + 1/x^2 )/x^2dx, t>= 0
note I = I(1) - I(0)

I'(t) = 2(0, ∞)∫1/(tx^2 + 1/x^2)dx

u = 1/x
-1/u^2du = dx

2(0, ∞)∫1/(x^4 + t)dx

t^1/4u = x
t^1/4du = dx

2t^1/4(0, ∞)∫1/(tx^4 + t)dx

= 2t^-3/4(0, ∞)∫1/(x^4 + 1)dx

integrate now from 0 to 1 or solve unparameterized integral

2t^-3/4(0, ∞)∫(1/x^2)/(x^2 + 1/x^2)dx

= 2t^-3/4(0, ∞)∫(1/x^2)/(x^2 + 1/x^2)dx

= t^-3/4(0, ∞)∫(2/x^2 + 1 - 1)/(x^2 + 1/x^2)dx

= t^-3/4[(0, ∞)∫(1 + 1/x^2)/((x - 1/x)^2 + 2)dx - (0, ∞)∫(1 - 1/x^2)/((x + 1/x)^2 - 2)dx]

let's find indefinite integrals with c = 0 to avoid interval problems

u = x + 1/x
du = (1-1/x^2)dx

v = x - 1/x
dv = (1 + 1/x^2)dx

∫1/(v^2 + 2)dv - ∫1/(u^2 - 2)du

2^1/2r = v
2^1/2dr = dv

2^1/2s = u
2^1/2ds = du

2^-1/2[∫1/(r^2 + 1)dr - ∫1/(s^2 - 1)ds]

= 2^-1/2[arctan(r) - 1/2∫1/(s - 1) - 1/(s + 1)ds]

= 2^-1/2arctan(2^-1/2(x - 1/x)) - 2^-3/2(log(2^-1/2(x + 1/x) + 1) - log(2^-1/2(x + 1/x) - 1)

= 2^-1/2arctan(2^-1/2(x - 1/x)) - 2^-3/2log((2^-1/2(x + 1/x) + 1)/(2^-1/2(x + 1/x) - 1)

now we can use result in original integral

t^-3/4[2^-1/2arctan(2^-1/2(x - 1/x))|(0, ∞) - 2^-3/2log((2^-1/2(x + 1/x) + 1)/(2^-1/2(x + 1/x) - 1) |(0, ∞)]

I'(t) = 2^-1/2t^-3/4

integrate from 0 to 1

(0, 1)∫I'(t)dt = (0, 1)∫2^-1/2t^-3/4dt

I(1) - I(0) = 2^3/2πt^1/4|(0, 1)

note I(1) - I(0) is our original integral

I = 2^3/2π

[stephyjose]

Can you help with the integral $\int_ {- \infty} ^ {\infty} dk\frac {e^ {-a\sqrt {s+\iota k}} e^ {-a\sqrt {s-\iota k}}} {(s+\iota k) (s-\iota k)} $ ?

[Dominikbeck]

I found another solution. Denote our integral as I. Second, denote N = int 4ln|x|/(1+x^2) dx from -infty to infty. This integral vanishes (as can be shown simply by x=1/y substitution). Then, you can perform by parts on I - N, giving you an expression I = 4 int (arctanx)/(x (x^4+1)) dx from -infty to infty. Let J = int_C ln (1+z)/(z(z^4+1)) dz, where ln has branch cut from -infty to -1. The contour C is C_1 U C_2, where C_1: z = it and C_2 = R e^(it) with t from -pi/2 to pi/2

[superkiller]

integrating from 0 up to infinity of ((ln(x^(2)+x+1))/(x^(2)+1)) dx. I would really appreciate it if you make a video about it. I managed to solve it from -inf to inf but i have no clue how to solve from 0 to inf

[TheRandomFool]

I've evaluated this before, but I actually used Feynman's technique to differentiate the logarithm under the integral sign. I then used contour integration on that. It's interesting to see how to evaluate it the way it is.

[Dominikbeck]

Try this: Integral (ln^2(x))/(x^4 + 1) from 0 to infty! (To solve this alternatively, I used the Feynman's method, differentiating the integral wrt a cleverly inserted parameter)

[TheHellBoy]

Sick video. Now do this again, but switch the quartic with the quadratic, and vice versa. I tried it and I messed up. And so, I turn to you. Love from India🔥🔥

[vascomanteigas]

The integral of exp(-x^2)/(x^2+1) along all real line equals to %e*%pi*erfc(1) and not %e*%pi as sugested by Residue Theorem due to essential singularity of exp(-x^2) at x=Infinity*%i. It can be bypassed, or the Feynmann technique are the only way ?

[captainkim]

Been looking for your new uploads. Thanks for the video.

P.S. I’m a former VCE student. :))

[karimshariff]

Nice video. Please write larger though. Thanks.

[zestyorangez]

studying for my complex prelim. ty for the resources ^-^