How Low Pass Filters Work

This video gives visual demonstrations of how capacitors and low pass filters work. It shows the circuit, the equations, the time-varying inputs and outputs, and the frequency response plot.

Start with visual of capacitor and current and voltage and time

Show applied DC voltage and voltage across capacitor

Note current initially flows until capacitor 'charges up' to source voltage level

Capacitor discharge in same time

Note that increasing capacitance makes it take longer to charge

Increased capacitance corresponds to decreased impedance per the equation

Which means it's not 'impeding' as much on stopping the current from flowing through it.

Discuss connection between temporal response and cutoff frequency

Go back to 10 u

Now instead of a DC input hear let's go with a square wave with 20 Hz

This is going to cycle between 5 V to –5 V 20 times a second, so one cycle every 50 ms.

Notice the voltage across the capacitor takes a little bit of time to follow this, but it catches up and is the same as the square wave most of the time

That means this signal at a frequency of 20 Hz would 'pass'.

Now let's crank this up to 85 Hz, which happens to be the cutoff frequency of this filter.

Notice that as soon as the capacitor 'catches up' to the source voltage, it gets switched. So at this frequency, the source signal might pass, but it will be attenuated since the voltage across the capacitor is spending most of the time 'catching up' to the changing source

Now let's crank this up to 500 Hz, which is beyond the cutoff frequency.

Now you can see the capacitor voltage never has enough time to 'catch up' with the alternating source voltage. So some of the signal would pass but it would be significantly attenuated

If we crank this up even further to 5 kHz you can see there is basically no response from our output voltage. The 5 kHz input square wave is (almost) completely cutoff.

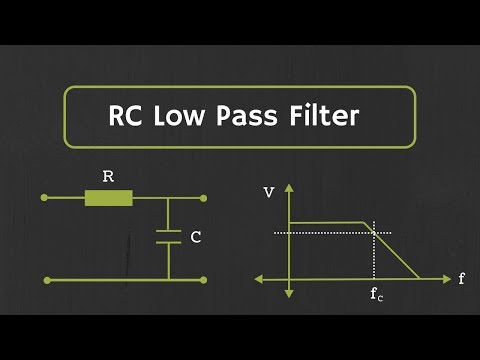
Now let's visualize what we've shown on a frequency response graph.

So here the x axis represents frequencies in a log scale, and the y axis represents how much of the source signal gets through to the ouput.

So if we go on this graph to the frequency we first showed of 20 Hz, you can see the the loss is small, and this is where our output signal was pretty close to the input signal

Then we go up to 80 hZ and you can see this curve has gone down a bit, this repsresents the –3dB where our output has lost about half the power of the input signal.

Then we go to 500 Hz and you can see it's further down,

And 5 kHz is of course further down still representing more attenuation of our source square wave

So you can see how this setup yields a low-pass filter, because it will pass the lower-frequency 20 Hz signal pretty closely, but will almost completely reject the 5 kHz squarewave.

So this is how a low pass filter works to allow lower frequencies and reject higher frequencies, and as discussed this is due to the time delay capacitors have with storing electrical energy.

If you were able to follow this, then you should have a good fundamental understanding of how capacitors and low pass RC filters work, and if you understand this, then it should be relatively straight forward to extend this understanding to how high-pass filters work, and to how filters using inductors instead of capacitors.

[BillChillson]

The best video on YouTube on this subject, thank you.

[stefangrozdanovic]

4 years of university study explained in a 8 minute video. Bravo sir!!

[PerishableDave]

Im trying to understand guitar pedal circuits and this video was incredibly helpful. Thanks!

[isagumus]

Matthew, amazing explanation and visualization. Thank you a lot!

[kennedn]

Very useful visualization and walkthrough, thank you.

[ChronicWhale]

Please consider making one of these for high pass filters as well

[harshvadhanas]

This comment is from India 🎉❤ thanks allot

[Russell_Huston]

So, if speaker leads are connected in parallel with the capacitor it functions as a low pass filter (NOT passing current until the cap is charged), and if you connect the speaker leads in series with the capacitor it functions as a high pass filter (passing current UNTIL the cap is charged). Do I understand that correctly?

[christianm]

Great explaination! Additionaly it would have been interesting to change the value of the resistor.
My question I ask myself is: which frequency should I set the filter for a DC Signal to filter out noise on the ADC input of my esp8266. Can it be too low? Ist it better to use a big resistor or a big capacitor to get a specific frequency?

[notaras]

Or you can have a mosfet acting as a switch right?

[ianfang]

Thanks for sharing, amazing video for explaining LPF.
Just curious, cut-off frequency should be the point at -3dB not the point at the critical point of 0dB.
In -3dB, Po/Pin = 1/2, that Vo/Vin = 0.707.
So red curve=Vo, Vo/Vin=(1 - e^(t/RC)) ramp-up to about 0.707 while being cross the green square pulse(Vin). That’s what I think of it but not pretty sure correct or not. Just for discussion, please correct me if any points I got wrong.

[turkishwithemre]

Hello thank you for the great information. İs it possible to learn the software that you use?

[chinmoyboruah]

It was really useful. Can you make one using an Op-Amp too?

[Ali_SRC]

Why does the 24VDC power supply act as a low-pass filter circuit?

[sss-ogjx]

hi Matthew, thanks for your video, I would like to know why is -3dB for cut off frequency?

[alexjohnson]

What happens to the filter if you increase the capacitance?

[PetakyahBuckley-htiz]

Why didn’t you use 10 µF? I thought that was the value of C. Instead you wrote 10 x 10^-6 s/n
I don’t get how you got that from 10 µF

[yuvavasu]

How capacitor is discharged when low inputs we provide

[Ali_SRC]

Why does the power supply act as a low-pass filter circuit?

[sachinkumar-rkdf]

which software are you using for making circuits