Finding Work using Calculus - The Cable/Rope Problem - Part b

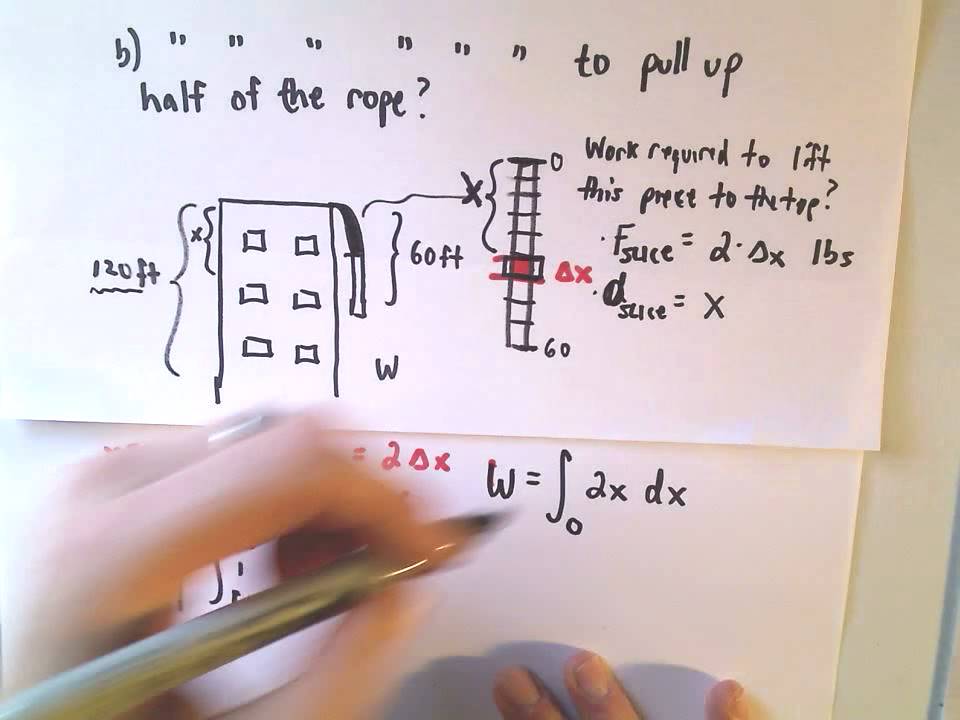
In this video, I find the work required to lift up only HALF of the rope to the top of the building.

[guest]

dude u shouldn't appolgise for anything while your making these videos, your saving alot of students in engineering like myself from hanging our selves, a fucking true hero

[findoneway]

Thank you so much. I was so frustrated with math problems. Watching your video made me feel more confident about math. Thank God bless you.

[patrickjmt]

@SonicGCT did not know it was, it is fixed now - thanks for letting me know.

[Sam-dcbg]

Oh now I get it, the bottom half of the rope is a constant 60 pounds...while the top is changing.

[TheSrrobinson]

I like the idea of doing it in one integral...it also helped to think of it like this: Integrate the work to life the entire rope (integrating 2xdx from 0 - 60) and then subtract out the work calculated by integrating 2xdx from 0 to 30. For one integral, it would be the integral of 2(60-xdx) from 0 to 30.

[nickschor]

Thanks again, Patrick.

Wonderful lesson!!

I now also know WHY we do these integrals...not just how. I feel....well....smarter!

[patrickjmt]

@bluejimmy168 it was set to private for some reason, sorry. it is available now!

[patrickjmt]

thanks.
just explaining things the way i understand them, is all

[patrickjmt]

@Bob8199 thanks! just tryin' my best here...

[choconiel]

today ill take my test for 25B and 25C your videos helped me a lot for those 2 tests :DDD watching ur videos and reading the book, i feel that i can conquer the world hahahhahaa thanks

[dustinchen]

man this guy explains it a million times better than my teacher does...

[anonymoususer]

Excellent work! I'd better check out other classes on your web site. I'm going to be a big fan of yours from now on.

[RyanLawrence]

if only all calculus teachers could explain stuff like you do, calculus would be much easier and less stressful

[kronikinsomniak]

@j5drumr the bottom half of the rope still has to move up, its all one piece, so you are adding the work required to move the bottom half up as well. You aren't just lifting half of the rope, but the WHOLE rope HALFWAY up.

[pmcate]

This can be solved less awkwardly by noting that the force as a function of x is (60-x)2. Then to find the work to pull half the rope you can integrate (60-x)2 dx from 0 to 30

[MicroTex]

Thanks Patrick, keep up the amazing work, awesome video

[ambdeyou]

thanks for your videos!they are always sooo helpful!

[johnferri]

Thank you for the very clear and detailed explanation. Could you do the same for this if possible: A chain is hanging from the ceiling (15' long, 3 lbs/ft). The ceiling is 20 ft high. What work is required to lift the bottom of the chain to the ceiling? (essentially, a doubled chain still hanging from the ceiling.) I've seen several explanations of this, but none as clear as yours. Thank you.

[Dleger]

it's still the same. If you change the upper bound to 70, you're left with integral(2x dx) from 0 - 35 + integral(2*35 dx) from 35 to 70. which gives you the same thing. unless you were referring to scenario where you're not pulling the rope up half way, in that case you're correct and it matters, but i guess i wasn't thinking about that when i wrote my comment. i've only ever dealt with pulling the rope up either halfway or the entire way.

[pvchio]

and besides, since we are only pulling the top half, it is weird that we need to calculate the bottom half, but anyway, thank you for his video. It is helpful