filmov
tv
What is the Fourier transform?

Показать описание
What is the Fourier transform?
What is the Fourier transform and why is everyone talking about it? In this video I present the Fourier transform and explain its relation with the Laplace transform and mention some of its applications. Moreover, I present some intuition behind the Fourier transform, which hopefully makes it easier to understand. Below you can find a link to a useful demo, which I also mention in this video. This is a must-see for anyone interested in partial differential equations or electrical engineering or signal processing.
What is the Fourier transform and why is everyone talking about it? In this video I present the Fourier transform and explain its relation with the Laplace transform and mention some of its applications. Moreover, I present some intuition behind the Fourier transform, which hopefully makes it easier to understand. Below you can find a link to a useful demo, which I also mention in this video. This is a must-see for anyone interested in partial differential equations or electrical engineering or signal processing.
But what is the Fourier Transform? A visual introduction.
An Introduction to the Fourier Transform
The Fourier Series and Fourier Transform Demystified
Fourier Transforms Explained Intuitively
Fourier Transform Equation Explained ('Best explanation of the Fourier Transform on all of YouT...
Introduction to the Fourier Transform (Part 1)
What is the Fourier Transform? ('Brilliant explanation!')
What is a Fourier Series? (Explained by drawing circles) - Smarter Every Day 205
Understanding the Discrete Fourier Transform and the FFT
Why do we use the Fourier Transform?
Fourier Transform, Fourier Series, and frequency spectrum
The Fourier Transform
|| What is fourier transformation || visualing short math clips || tranformation ||
Introduction to Fourier Transform
What is the Fourier Transform used for?
The intuition behind Fourier and Laplace transforms I was never taught in school
What is the difference between the Fourier Series and Fourier Transform?
Fourier Transform Explained
Electrical Engineering: Ch 19: Fourier Transform (1 of 45) What is a Fourier Transform?
Fourier series
Fourier Transform Maths Explained #fouriertransform #maths #mathematics
But what is a Fourier series? From heat flow to drawing with circles | DE4
To Understand the Fourier Transform, Start From Quantum Mechanics
Introduction to Fourier Transform
Комментарии
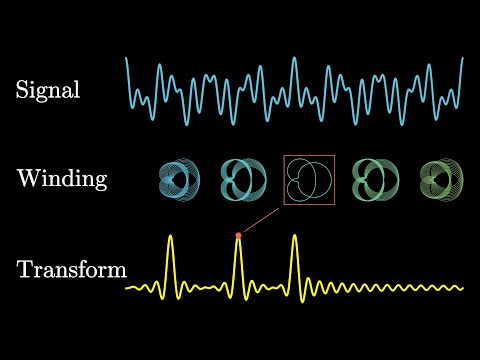 0:20:57
0:20:57
 0:03:20
0:03:20
 0:14:48
0:14:48
 0:09:48
0:09:48
 0:06:26
0:06:26
 0:13:03
0:13:03
 0:13:37
0:13:37
 0:08:25
0:08:25
 0:19:20
0:19:20
 0:00:59
0:00:59
 0:15:46
0:15:46
 0:14:36
0:14:36
 0:00:24
0:00:24
 0:08:19
0:08:19
 0:09:35
0:09:35
 0:18:00
0:18:00
 0:00:56
0:00:56
 0:09:09
0:09:09
 0:06:21
0:06:21
 0:01:00
0:01:00
 0:00:59
0:00:59
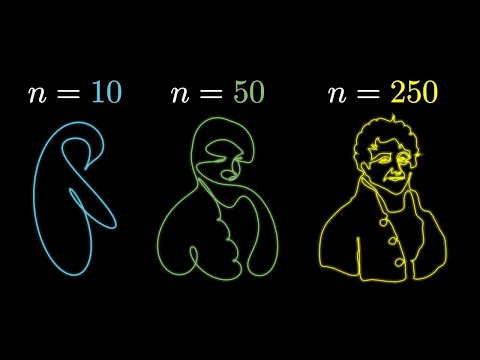 0:24:47
0:24:47
 0:31:37
0:31:37
 0:06:22
0:06:22