filmov
tv
Intuition is Essential to Problem Solving
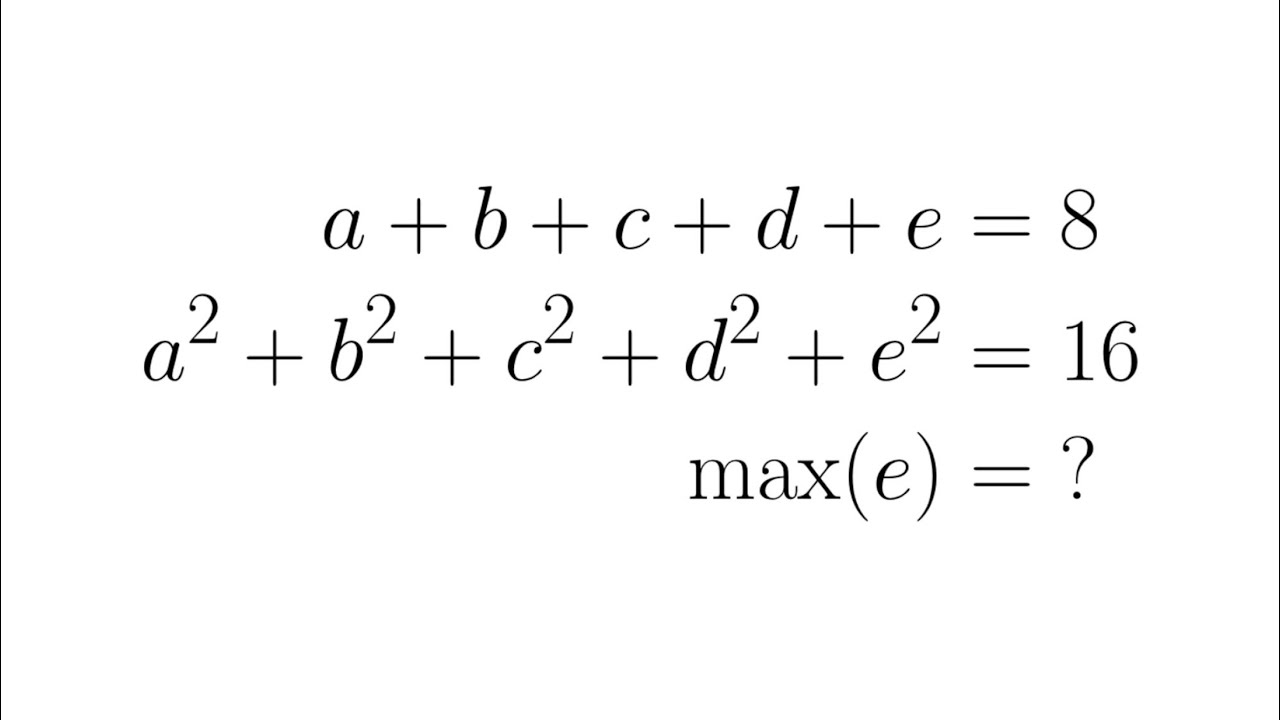
Показать описание
#Math #Algebra #inequality
In this video we solve a problem modified from one in the Singaporean Maths Olympiad.
Subscribe @letsthinkcritically !!
————————————————————————————————————————————————
I share Maths problems and Maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
In this video we solve a problem modified from one in the Singaporean Maths Olympiad.
Subscribe @letsthinkcritically !!
————————————————————————————————————————————————
I share Maths problems and Maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
Intuition is Essential to Problem Solving
Unlocking Your Intuition: How to Solve Hard Problems Easily
Should You Trust Your Gut Instinct?
What is Intuition | Explained in 2 min
Check your intuition: The birthday problem - David Knuffke
When (not) to use intuition?
Math and Intuition
The essence of calculus
This tool will help improve your critical thinking - Erick Wilberding
KRUPS Intuition Essential - czyszczenie ekspresu
Unlocking Your Intuition: How to Solve Hard Problems Easily
Introverted Intuition - from Carl Jung's Psychological Types
Harnessing intuition for solving hard problems
Intuition Tip - The Knowing vs Mind Thoughts
Intuition is the supra-logic that cuts out all = Robert Graves
Critical Thinking and Intuition in a Post-Truth Society
Solve all your Problems Easily by Developing your Intuition, Here is How..(Amazing Advice!)
WILL I EVER LEARN?!? 🤣Intuition has never been wrong.
Intuition vs. Thought: Which One Guides You?
Supercharge Your Intuition in 15 Seconds a Day
Signs it is your intuition talking #shorts #youtubeshorts #intuition #innerpeace #intuitive
Good Intuition
Why Use Your Intuition to Solve Business Problems?
Moral Reasoning vs. Moral Intuition | Ethical Decision Making | Ethics101 | UPSC GS IV Ethics
Комментарии
 0:06:36
0:06:36
 0:17:34
0:17:34
 0:04:25
0:04:25
 0:02:13
0:02:13
 0:05:07
0:05:07
 0:00:37
0:00:37
 0:00:58
0:00:58
 0:17:05
0:17:05
 0:05:20
0:05:20
 0:01:50
0:01:50
 0:04:21
0:04:21
 0:05:26
0:05:26
 0:03:03
0:03:03
 0:01:00
0:01:00
 0:00:12
0:00:12
 0:00:57
0:00:57
 0:12:21
0:12:21
 0:00:05
0:00:05
 0:06:18
0:06:18
 0:00:38
0:00:38
 0:00:52
0:00:52
 0:01:00
0:01:00
 0:01:37
0:01:37
 0:13:55
0:13:55