filmov
tv
How to Prove that the Intersection of Subspaces of a Vector Space is a Subspace

Показать описание
How to Prove that the Intersection of Subspaces of a Vector Space is a Subspace
How To Prove The Quran Has Been Preserved Accurately
How to Prove Trigonometric Identities (and how not to)
How to Prove a Function is Injective(one-to-one) Using the Definition
How to Prove Math Theorems | 1st Ex: Even + Odd = Odd
Direct Proof: Prove that if 5x - 7 is odd, then 9x + 2 is even
How to Prove That a Quadrilateral Is a Parallelogram With Diagonals : Parallelograms & Math
How to Prove that the Interval (a, b] is Not an Open Set
How to Prove that a Matrix is Positive Definite
How to prove that the limit does not exist (KristaKingMath)
Learn how to use mathematical induction to prove a formula
How To Prove That Jesus Is God To A Muslim
How to Prove that the Natural Logarithm is an Onto Function
GCSE Maths - How to Prove Algebraic Identities - Proof Part 2 #63
how to prove that log_2(3) is irrational by using contradiction
How to Prove that the Limit of (2n + 1)/(3n + 7) as n approaches infinity is 2/3
How to Prove that the Derivative of a Constant is Zero(0) - Calculus
Learn How To Prove A Trigonometry Question & Apply Trig Identities Effectively
How to Prove a Function is Surjective(Onto) Using the Definition
Proof 1+1=11 || Prove that 1+1=11 || How to prove 1+1=11 || Funny math proof
Connected Classrooms: How to Prove That 1 = 2 with Mathematician James Tanton
Only U.S. President to prove a theorem
How to prove that the empty set is a subset of any set
How to Prove that a Quadratic Function is Always Positive (or Negative)
Prove that 2=3 || How To Proof 2=3
Комментарии
 0:08:03
0:08:03
 0:07:37
0:07:37
 0:03:35
0:03:35
 0:08:35
0:08:35
 0:03:54
0:03:54
 0:05:01
0:05:01
 0:04:54
0:04:54
 0:06:52
0:06:52
 0:06:04
0:06:04
 0:07:08
0:07:08
 0:07:45
0:07:45
 0:03:16
0:03:16
 0:04:37
0:04:37
 0:03:56
0:03:56
 0:11:39
0:11:39
 0:03:31
0:03:31
 0:13:17
0:13:17
 0:03:44
0:03:44
 0:01:58
0:01:58
 0:47:30
0:47:30
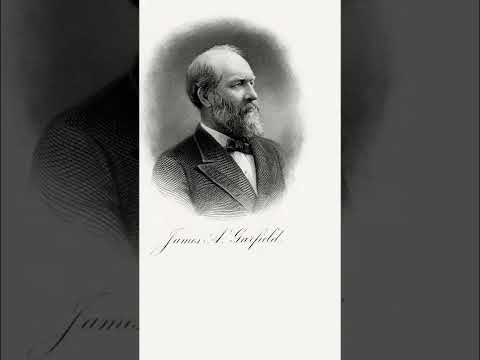 0:01:00
0:01:00
 0:02:43
0:02:43
 0:04:15
0:04:15
 0:02:47
0:02:47