filmov
tv
GT11.1. Automorphisms of A4

Показать описание
Abstract Algebra: We compute the automorphism group of A4, the alternating group on 4 letters. We have that Aut(G) = S4, the symmetric group on 4 letters, Inn(A4) = A4, and Out(A4)=Z/2. We note that the coset structure splits S4 into even and odd permutations.
GT11.1. Automorphisms of A4
GT11. Group Automorphisms
Group Automorphism
What does automorphism mean?
MATH 430 — 12: Automorphisms
GT12.1. Automorphisms of Dihedral Groups
Example of Group Automorphism 1 (Requires Linear Algebra)
Group Theory 31, Automorphisms and Inner Automorphisms
Visual Group Theory, Lecture 4.6: Automorphisms
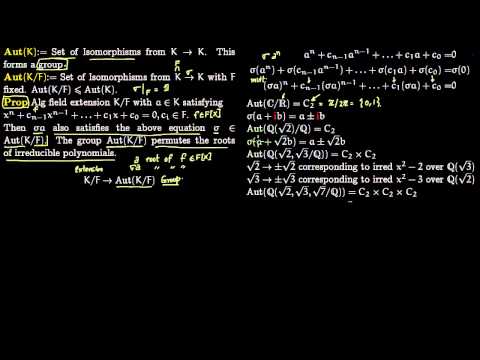
Abstract Algebra II: automorphisms and fixed subfields, 3-20-19
Group Theory 30, Automorphisms
Automorphism groups and modular arithmetic
FIT4.2. Automorphisms and Degree
Automorphism
Abstract Algebra, Lecture 15A: Review Aut(G) and Inn(G), Properties of Cosets and Proof Sketches
Abstract Alg, Lec 16A: Aut(G) & Inn(G) are Invariants, Converse of Lagrange, Sylow's First ...
Lec 1 Edge automorphisms of graphs
Example of Group Automorphism 2: G = Z/4 x Z/4 (Requires Linear Algebra)
AGT: Automorphisms of direct products of some circulant graphs
Group Automorphisms Part 1
Aut(Zn) | The group of Automorphisms | Group Theory
2.10 Automorphisms
A4 Properties of Algebra
lec#66 Alternating group of degree 'n' full detail #group #theory #mathematics #lecture #p...
Комментарии
 0:11:01
0:11:01
 0:25:02
0:25:02
 0:09:58
0:09:58
 0:00:37
0:00:37
 0:23:13
0:23:13
 0:25:58
0:25:58
 0:17:36
0:17:36
 0:22:16
0:22:16
 0:24:34
0:24:34
 0:50:06
0:50:06
 0:14:16
0:14:16
 0:17:56
0:17:56
 0:14:47
0:14:47
 0:11:35
0:11:35
 0:37:49
0:37:49
 0:33:00
0:33:00
 0:34:47
0:34:47
 0:11:23
0:11:23
 0:50:07
0:50:07
 0:27:27
0:27:27
 0:32:13
0:32:13
 0:27:08
0:27:08
 0:11:22
0:11:22
 0:25:10
0:25:10