Simplifying fractions with examples and practice questions | GCSE Maths Foundation

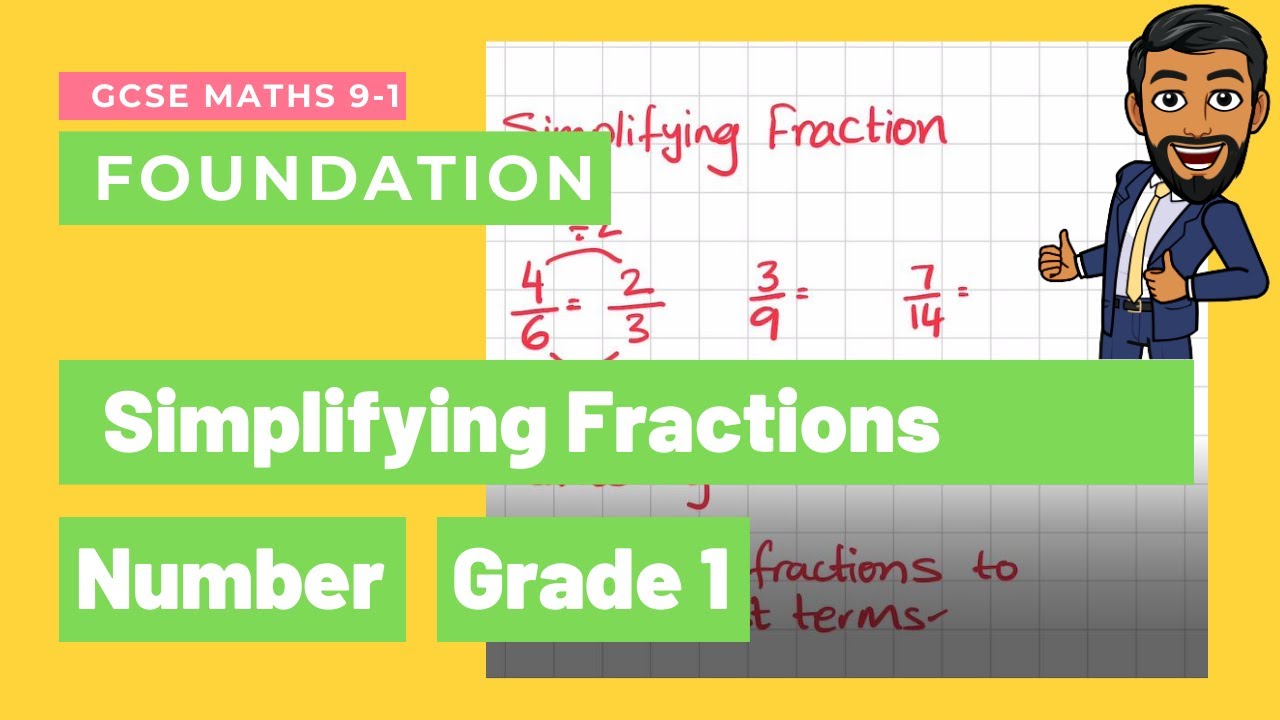
SImplifying fractions is a common questions in GCSE Maths Foundation exam. A good way to simplify fractions is by dividing by the highest common factor. If you are not sure how to find the HCF then the alternative way is to divide the numerator and denominator until you find the lsimplest form.

Here are the steps to simplify fractions:
Write down the factors for the numerator and the denominator.
Find the highest common factor of the numerator and the denominator.
Divide the numerator and denominator by the highest common factor.
Write down the simplified fraction.

I have also included some practice questions at the end of the video with answers. So have a go atthose questions to test your understanding.

Tiktok quick Maths: @mrmahmudmaths
I wish you all the best for your GCSE Maths exams. Mr Mahmud, helping you do better in Maths. :)
#gcsemaths #mathsrevision #gcse

GCSE Maths revision guides and workbooks: Affiliate links

[saadakilmi]

my techar i want toturial frection videos

[iqfncmq]

HOW TO SIMPLIFY FRACTIONS THE EASIEST WAY:
If the difference between the numerator and denominator is 1, the fraction cannot be simplified.
A. Ask: does the numerator go into the denominator evenly (i.e. without any remainder)?
If yes, proceed to B.
If not, proceed to C.
B. Great! The simplest fraction is 1 over the number of times the numerator fits in the denominator. (e.g. 20/60, 20 fits evenly 3 times, hence 1/3.)
C. Write the remainder, (e.g. 20/46, (20 fits 2 times in 46, with a remainder of) 6.) to the right of the fraction, and ask: does the remainder go evenly into the numerator?
If yes, proceed to D.
If not, proceed to E.
D. Great! The "remainder" is the Greatest Common Factor. Divide both the numerator and denominator by the GCF/remainder to have the simplest fraction.
E. Write the "new remainder" (using the last example, 20/46, 6 fits into 20 with a "new remainder" of 2) to the right of the previous "remainder", and ask: does the "new remainder" fit evenly into the previous "remainder" (2 into 6)?
If yes, proceed to D.
If not, proceed to E.
Please, (with your amazing talent, ) produce a video demonstrating it.

//Euclidean Algorithm.