filmov
tv
Ex 1: Evaluate a Double Integral Over a Rectangular Region to Find a Volume - f(x,y)=c

Показать описание
This video explains how to determine the value of a double integral that represents volume. A geometric formula is used the the double integral is evaluated.
Ex 1: Evaluate a Double Integral Over a Rectangular Region to Find a Volume - f(x,y)=c
Ex 1 : Evaluate a Double Integral Over a Rectangular Region to Find a Volume fx,y=c
Ex - Evaluate a Double Integral Over a Rectangular Region fx,y=ax+by
Ex: Evaluate a Double Integral to Determine Volume (Basic)
Ex: Evaluate a Double Integral to Determine Volume - Change Order of Integration
Evaluate the integral by reversing the order of integration
Ex: Evaluate a Double Integral Over a Rectangular Region to Find a Volume - f(x,y)=ax
Ex: Evaluate a Double Integral Over a Rectangular Region - f(x,y)=ax+by
Sketch the Region, Reverse the order and evaluate the limit of integration || Thomas Calculus | 15.2
Evaluate a Double Integral Over a General Region - f(x,y)=xy^2
Evaluate Double and Half Angles Ex #1
Evaluation of double integral over the region parabola and straight lines /( Cartesian coordinates)
Evaluate a double integral involving trig function.
Ex: Evaluate a Double Integral Over a Rectangular Region to Find a Volume - f(x,y)=x/y
#4 Evaluation of Double integral changing the order of integration 22MATX21|VTU|SUK|21MAT21|18MAT21
Evaluate a Double Integral Using Substitution Over a Rectangular Region - f(x,y)=(ax+by)^n
Example-1 Direct evaluation of double Integral
Ex 1: Using Stoke's Theorem to Evaluate a Surface Integral as a Line Integral
Ex 2: Evaluate a Double Integral Over a Rectangular Region to Find a Volume - f(x,y)=constant
Evaluation of Double Integral by changing it into Polar coordinates
Evaluation of double integral by change of variables problem
Evaluation of double integrals by changing order of integration. Class 1.Introduction and example.
Use Symmetry to evaluate Double Integral: /(1+x^2*sin(y) + y^2*sin(x)) dy dx, y = x = -pi to pi
VTU Engineering Maths 1 Evaluate double integration of xy over the positive quadrant of the circle
Комментарии
 0:03:21
0:03:21
 0:03:26
0:03:26
 0:04:59
0:04:59
 0:03:40
0:03:40
 0:07:38
0:07:38
 0:08:15
0:08:15
 0:04:12
0:04:12
 0:04:10
0:04:10
 0:33:27
0:33:27
 0:06:46
0:06:46
 0:09:24
0:09:24
 0:14:40
0:14:40
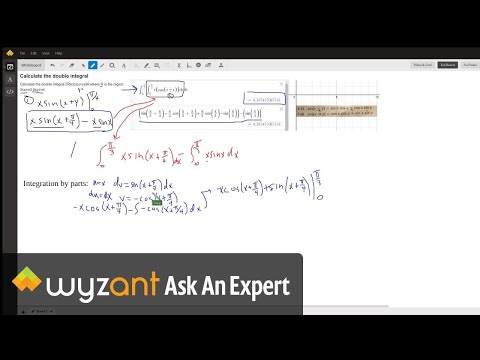 0:04:54
0:04:54
 0:04:53
0:04:53
 0:13:17
0:13:17
 0:06:51
0:06:51
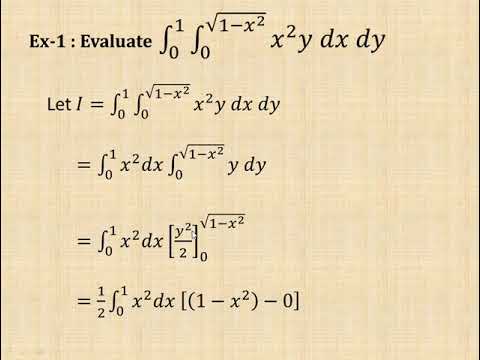 0:03:01
0:03:01
 0:07:41
0:07:41
 0:04:20
0:04:20
 0:06:47
0:06:47
 0:11:18
0:11:18
 0:10:02
0:10:02
 0:02:58
0:02:58
 0:04:44
0:04:44