filmov
tv
Evaluation of double integral over the region parabola and straight lines /( Cartesian coordinates)

Показать описание
Evaluation of double integral over the region parabola and straight lines /( Cartesian coordinates)
00:00 Introduction
02:15 finding intersection of points
04:21 evaluation of integration over the limits
Dear students, based on students request , purpose of the final exams, i did chapter wise videos in PDF format, if u are interested, you can download Unit wise videos by clicking the below links
TEAM Education
• 3 hours ago
Click the links
Unit 1:ODE First order Differential Equations
Unit 2: Higher order DE.
Unit 3: Multiple Integrals
Unit 4:Vector Differential Calculus
Unit 5:Vector Integral Calculus Part 1
Unit 6: Vector Integral Calculus Part 2
Unit 7: Special Functions
Beta & Gamma Functions
Unit 8: Functions of Single Variables
Unit 1: First Order ODE- Playlist
Unit 2:ODE of Higher Order- Playlist
Unit 3: Multi Variable Calculus-(Integration)-Playlist
Unit 4: Vector Differentiation-Playlist
Unit 5: Vector Integration-Playlist
n this chapter we also discussing Double Integrals in Cartesian & polar Coordinates, Triple Integrals in Cartesian & Cylindrical Coordinates and Spherical Coordinates,
Evaluation of Double integral,
Double integral with independent limits,
Double integral without limits,
Triple Integrals,
Double integral with one dependent limits,
Evaluation of Triple integral,
Triple integral with independent limits,
Triple integral with dependent limits,
Evaluation of Integrals by Change of Variables,
Evaluation of Integrals by Change of Order of Integration,
Double Integrals in polar Coordinates
Double Integrals in polar Coordinates with independent limits,
Double Integrals in polar Coordinates with dependent limits,
evaluation of Triple integrals by changing into spherical coordinates,
evaluation of Triple integrals by changing into cylindrical coordinates
00:00 Introduction
02:15 finding intersection of points
04:21 evaluation of integration over the limits
Dear students, based on students request , purpose of the final exams, i did chapter wise videos in PDF format, if u are interested, you can download Unit wise videos by clicking the below links
TEAM Education
• 3 hours ago
Click the links
Unit 1:ODE First order Differential Equations
Unit 2: Higher order DE.
Unit 3: Multiple Integrals
Unit 4:Vector Differential Calculus
Unit 5:Vector Integral Calculus Part 1
Unit 6: Vector Integral Calculus Part 2
Unit 7: Special Functions
Beta & Gamma Functions
Unit 8: Functions of Single Variables
Unit 1: First Order ODE- Playlist
Unit 2:ODE of Higher Order- Playlist
Unit 3: Multi Variable Calculus-(Integration)-Playlist
Unit 4: Vector Differentiation-Playlist
Unit 5: Vector Integration-Playlist
n this chapter we also discussing Double Integrals in Cartesian & polar Coordinates, Triple Integrals in Cartesian & Cylindrical Coordinates and Spherical Coordinates,
Evaluation of Double integral,
Double integral with independent limits,
Double integral without limits,
Triple Integrals,
Double integral with one dependent limits,
Evaluation of Triple integral,
Triple integral with independent limits,
Triple integral with dependent limits,
Evaluation of Integrals by Change of Variables,
Evaluation of Integrals by Change of Order of Integration,
Double Integrals in polar Coordinates
Double Integrals in polar Coordinates with independent limits,
Double Integrals in polar Coordinates with dependent limits,
evaluation of Triple integrals by changing into spherical coordinates,
evaluation of Triple integrals by changing into cylindrical coordinates
Комментарии
 0:25:02
0:25:02
 0:15:29
0:15:29
 0:04:29
0:04:29
 0:11:10
0:11:10
 0:17:52
0:17:52
 0:16:37
0:16:37
 0:08:56
0:08:56
 0:17:27
0:17:27
 0:26:40
0:26:40
 0:41:28
0:41:28
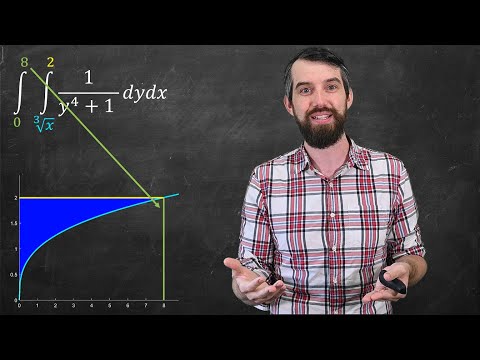 0:07:39
0:07:39
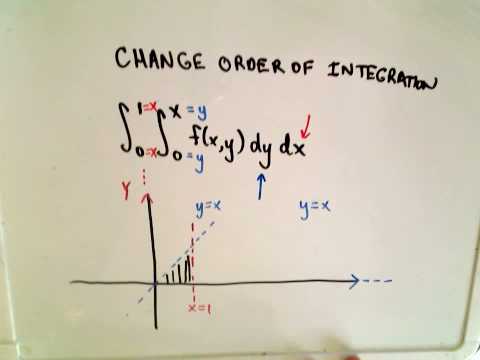 0:04:20
0:04:20
 0:02:22
0:02:22
 0:10:32
0:10:32
 0:03:21
0:03:21
 0:17:29
0:17:29
 0:12:44
0:12:44
 0:12:16
0:12:16
 0:04:18
0:04:18
 0:05:03
0:05:03
 0:09:13
0:09:13
 0:07:30
0:07:30
 0:11:40
0:11:40
 0:08:36
0:08:36