filmov
tv
The limit of limiting arguments

Показать описание
A link to the full video is at the bottom of the screen.
That video gives multiple examples of lying with visual proofs
Editing from the original video into this short by Dawid Kołodziej
That video gives multiple examples of lying with visual proofs
Editing from the original video into this short by Dawid Kołodziej
The limit of limiting arguments
Limiting Arguments and Derivatives by First Principles
Limitations of limiting arguments
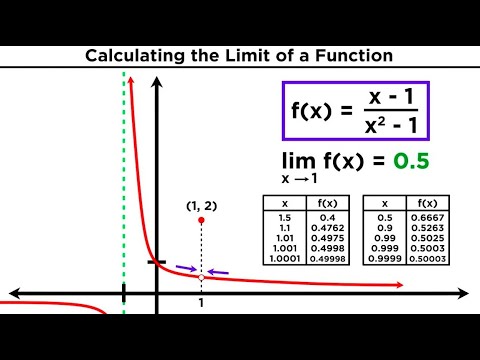
Limits and Limit Laws in Calculus
How To Find The Limit At Infinity
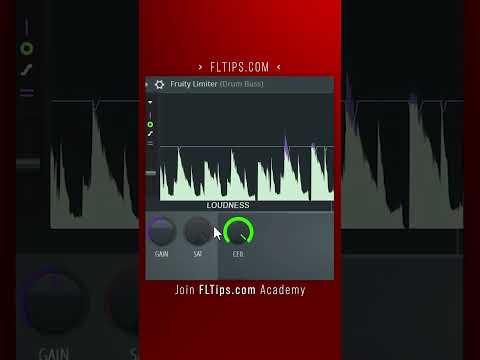
Biggest Limiting Mistake | FL Studio Tutorial #shorts
Limits of Multivariable Functions - Calculus 3
Limits of Trigonometric Functions
Statistical distributions full course session 43
Piecewise Functions - Limits and Continuity | Calculus
Limits at Infinity & Horizontal Asymptotes
Stop limiting God. #god #jesus #shorts
PMVW01 | Prof. Gregory Grason | Geometrically frustrated assembly: Limits of self-limitation
Lecture : 14 Limiting behaviour of measurable functions
Argue For or Against the Limitation of Speed Limits - Essay Example
Advanced Rate Limiting with NGINX Plus Ingress Controller
3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus
The Art of Taming Peaks: Manual Limiting Techniques for Louder Masters! #masteringengineer #producer
Motivating Limits (or Limiting Values)
John Stuart Mill, On Liberty | Limiting Intemperate Discussion | Philosophy Core Concepts
Talking Business: The limits of a limitation of liability clause
Why use Current Limiting Resistors | AddOhms #8
Turn OFF True Peak Limiting! FabFilter Pro L2 Trick
Examination Argue for or Against the Limitation of Speed Limits
Комментарии
 0:00:51
0:00:51
 0:12:42
0:12:42
 0:00:47
0:00:47
 0:12:49
0:12:49
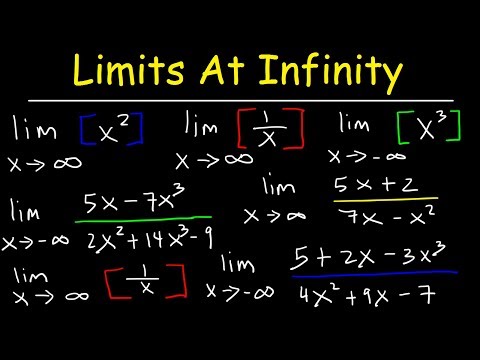 0:13:14
0:13:14
 0:00:26
0:00:26
 0:19:04
0:19:04
 0:15:23
0:15:23
 11:55:00
11:55:00
 0:10:06
0:10:06
 0:19:24
0:19:24
 0:00:25
0:00:25
 0:34:36
0:34:36
 0:43:48
0:43:48
 0:05:58
0:05:58
 0:02:27
0:02:27
 0:10:10
0:10:10
 0:00:44
0:00:44
 0:05:58
0:05:58
 0:17:24
0:17:24
 0:24:23
0:24:23
 0:05:10
0:05:10
 0:00:44
0:00:44
 0:00:45
0:00:45