filmov
tv
Lesson 17: Geometric Distribution Part 1

Показать описание
Introduction to Geometric Distribution. We give an intuitive introduction to the geometric random variable, outline its probability mass function, and cumulative distribution function.
Lesson 17: Geometric Distribution Part 1
Lesson 17: Geometric Distribution part II
Chapter 17 Notes Part 1 Geometric Distribution 2019
Geometric Distribution EXPLAINED with Examples
Geometric Example
Chapter 17 D1 Geometric Probability Model
Geometric Distribution - Probability, Mean, Variance, & Standard Deviation
AP Stats: Ch 17 Geometric and Binomial Distributions
A Level Statistics 2.11 The Geometric Distribution
Geometric Distributions and The Birthday Paradox: Crash Course Statistics #16
Hypothesis Testing with a Geometric Distribution
Chapter 17 Notes Part 2 Binomial and Geometric CUMULATIVE; Expected Values
Geometric Distribution
11/17/21 - Geometric Distribution (Part 1)
Chapter 17 Notes Part 1 Binomial and Geometric PDF
[MATH] Statistics 1 | Geometric distribution | Part 1
AP Stats: Ch 17 Geometric and Binomial Distributions
Statistics: Geometric Probability Distribution
Geometric Distribution
Statistics: Introduction to Geometric Distribution Probabilities
4.3.17 Geometric Distribution using StatCrunch Trials Calculator
Geometric Distribution - Derivation of Mean, Variance & Moment Generating Function (English)
[Chapter 4] #17 Negative Binomial distribution and properties
Maths with motivation || Geometric Distribution || Success vs Failure || @17matboy
Комментарии
 0:15:45
0:15:45
 0:24:40
0:24:40
 0:27:37
0:27:37
 0:07:08
0:07:08
 0:06:21
0:06:21
 0:22:25
0:22:25
 0:32:13
0:32:13
 0:17:37
0:17:37
 0:06:38
0:06:38
 0:10:19
0:10:19
 0:06:22
0:06:22
 0:47:09
0:47:09
 0:04:58
0:04:58
 0:29:20
0:29:20
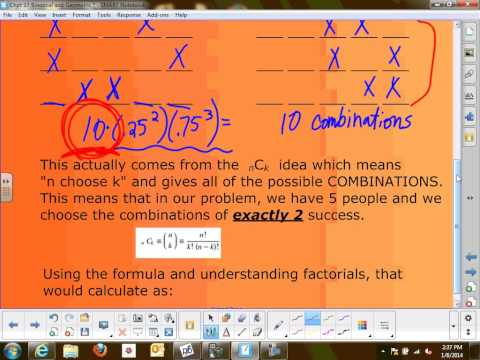 0:39:13
0:39:13
![[MATH] Statistics 1](https://i.ytimg.com/vi/37ZQilYbW1s/hqdefault.jpg) 0:12:44
0:12:44
 0:17:45
0:17:45
 0:02:02
0:02:02
 0:30:25
0:30:25
 0:08:16
0:08:16
 0:04:55
0:04:55
 0:24:04
0:24:04
![[Chapter 4] #17](https://i.ytimg.com/vi/7Q42ujSxys8/hqdefault.jpg) 0:07:59
0:07:59
 0:00:55
0:00:55