filmov
tv
Finding the Real Solution | Exponential Equation | 5^x +5^3x = 10

Показать описание
#solvingexponentialequation #exponentialequation #howtosolveexponentialequation
In this video, we will solve this nice exponential 5^x +5^3x = 10. This is unusual exponential equation and we will find the real solution
In this video, we will solve this nice exponential 5^x +5^3x = 10. This is unusual exponential equation and we will find the real solution
How To Find The Real & Imaginary Solutions of Polynomial Equations
How to find the solutions of a quadratic using the quadratic formula
How to find the discriminant and label the solutions of a quadratic
How to Determine the Number of Real and Nonreal Solutions for a Quadratic Equation
How To Determine The Discriminant of a Quadratic Equation
Solving using the quadratic formula with complex solutions
Find all the solutions of a rational equation and check your solution
Find range of k for quadratic equation to have real solution
Solve quadratic equation
What is a 'Solution Set' for an Equation (Algebra)
Quadratic Equations | Solve by factoring | Free Math Videos
Number of solutions to linear equations | Linear equations | Algebra I | Khan Academy
How to find the roots of a polynomials by factoring
An Equation with Real Solutions
Quadratic formula with imaginary numbers
How to Prove an Equation Has a Real Solution using the Intermediate Value Theorem
Solving Equations With Complex Numbers
How To Solve Quadratic Equations Using The Quadratic Formula
How to identify the number of solutions using the discriminant of a quadratic
Solving An Equation for Real Solutions
Quadratic Equations With No Real Solution
Find K For Different Number of Solution of Quadratic Equation
Checking For Extraneous Solutions of Radical Equations
One Solution, No Solution, or Infinitely Many Solutions - Consistent & Inconsistent Systems
Комментарии
 0:12:52
0:12:52
 0:05:24
0:05:24
 0:02:34
0:02:34
 0:05:06
0:05:06
 0:03:05
0:03:05
 0:05:28
0:05:28
 0:04:27
0:04:27
 0:04:56
0:04:56
 0:11:58
0:11:58
 0:02:36
0:02:36
 0:02:43
0:02:43
 0:05:27
0:05:27
 0:02:43
0:02:43
 0:06:47
0:06:47
 0:11:52
0:11:52
 0:07:11
0:07:11
 0:02:07
0:02:07
 0:05:56
0:05:56
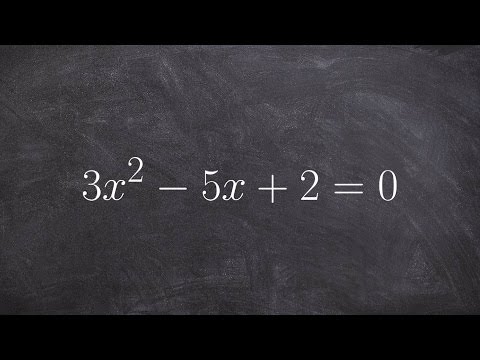 0:02:18
0:02:18
 0:09:22
0:09:22
 0:04:50
0:04:50
 0:04:47
0:04:47
 0:10:22
0:10:22
 0:07:30
0:07:30