filmov
tv
A Nice Rational Equation Challenge | The Olympiad Approach
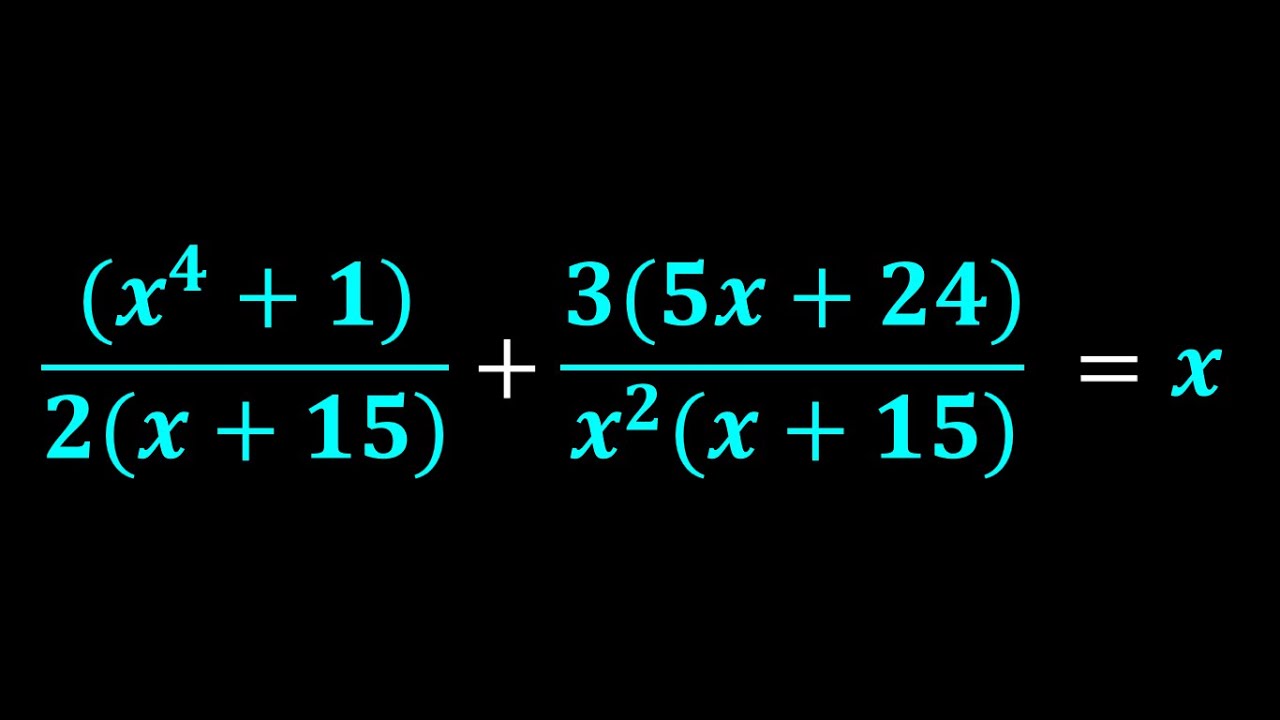
Показать описание
A Nice Rational Equation Challenge | The Olympiad Approach
Get ready to tackle an amazing rational equation challenge. In this algebraic video, we'll explore a fascinating rational equation that will upgrade mathematical skills and problem-solving abilities. Perfect for those preparing for math competitions or anyone who enjoys a good challenge, this problem will stretch your thinking and help you develop your algebra skills. Watch the video, try solving the equation, and share your solutions in the comments below. Don't forget to like, subscribe, and hit the notification bell for more challenging math content!
In this tutorial, you'll learn:
1- Fundamental concepts and definitions of rational equations
2- Step-by-step methods to solve challenging rational equations
3- Common pitfalls and how to avoid them
4- Expert tips and tricks for solving problems quickly and accurately
5- Practice problem with detailed solutions
Additional Resources:
#matholympiad #rationalequations #mathtutorial #problemsolving #matholympiadpreparation #learnmath #education #algebra #math
Join us as we unlock the secrets to excelling in rational equations and take your Math Olympiad prep to the next level. Don't forget to like, subscribe, and hit the bell icon for more Math Olympiad prep videos. Let's conquer those equations together!
Thanks for Watching!!
@infyGyan
Get ready to tackle an amazing rational equation challenge. In this algebraic video, we'll explore a fascinating rational equation that will upgrade mathematical skills and problem-solving abilities. Perfect for those preparing for math competitions or anyone who enjoys a good challenge, this problem will stretch your thinking and help you develop your algebra skills. Watch the video, try solving the equation, and share your solutions in the comments below. Don't forget to like, subscribe, and hit the notification bell for more challenging math content!
In this tutorial, you'll learn:
1- Fundamental concepts and definitions of rational equations
2- Step-by-step methods to solve challenging rational equations
3- Common pitfalls and how to avoid them
4- Expert tips and tricks for solving problems quickly and accurately
5- Practice problem with detailed solutions
Additional Resources:
#matholympiad #rationalequations #mathtutorial #problemsolving #matholympiadpreparation #learnmath #education #algebra #math
Join us as we unlock the secrets to excelling in rational equations and take your Math Olympiad prep to the next level. Don't forget to like, subscribe, and hit the bell icon for more Math Olympiad prep videos. Let's conquer those equations together!
Thanks for Watching!!
@infyGyan
Комментарии
 0:12:44
0:12:44
 0:13:14
0:13:14
 0:02:09
0:02:09
 0:02:08
0:02:08
 0:13:14
0:13:14
 0:00:55
0:00:55
 0:13:01
0:13:01
 0:08:21
0:08:21
 0:01:01
0:01:01
 0:10:46
0:10:46
 0:09:24
0:09:24
 0:15:50
0:15:50
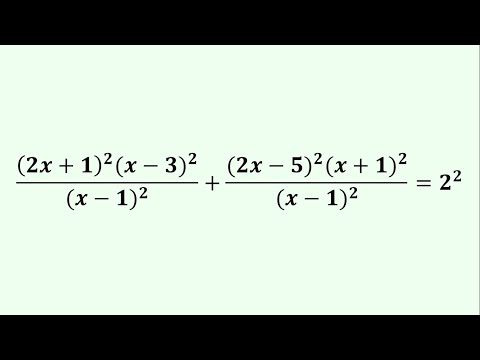 0:13:54
0:13:54
 0:01:43
0:01:43
 0:00:52
0:00:52
 0:10:55
0:10:55
 0:02:22
0:02:22
 0:14:26
0:14:26
 0:08:20
0:08:20
 0:04:35
0:04:35
 0:12:37
0:12:37
 0:00:37
0:00:37
 0:11:20
0:11:20
 0:17:42
0:17:42