Linear Programming & Combinatorial Optimization (2022) Lecture-40

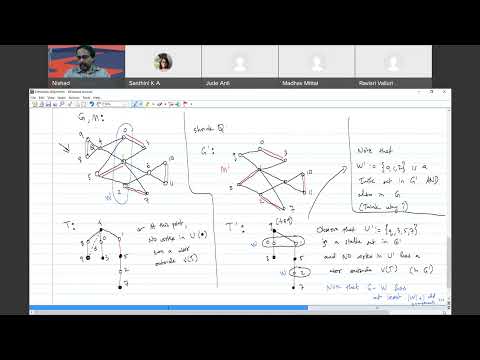
In today's lecture (07/04/2022), we considered the LP relaxation (for Min Cost Perfect Matching Problem) proposed by Edmonds (1965). This (as we discussed yesterday) LP, say (P), has three types of constraints: (i) non-negativity, (ii) degree, and the additional (iii) ODD CUT constraints.

We wrote down the dual (D), the Complementary Slackness (CS) conditions, as well as their combinatorial interpretations. In particular, we got two CS conditions, say (1) and (2).

Thereafter, we imitated the Hungarian Algorithm (for bipartite Min Cost PM Problem) in order to develop a similar algorithm (for the nonbipartite case). In particular, instead of using deficient sets, we use Tutte sets. We will continue from here tomorrow (08/04/2022), and we will notice that it's not quite easy to ensure the CS condition (2).