Linear Programming & Combinatorial Optimization (2022) Lecture-37

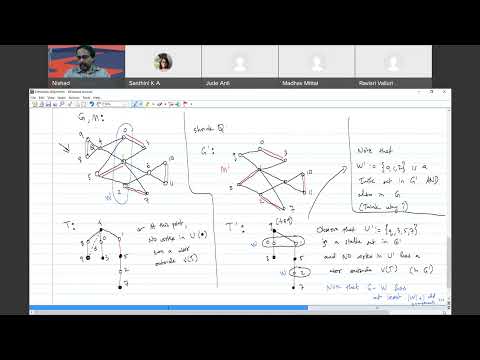
In today's lecture (01/04/2022), we covered a relatively big example (20 vertices) of Edmonds' Blossom Algorithm --- to find a perfect matching in a general (i.e., not necessarily bipartite) graph (if one exists).

Edmonds' referred to each shrunken odd cycle as a blossom --- hence, the name.

In today's example (graph G and matching M), after shrinking multiple blossoms, we found an augmenting path in the last "derived graph".

In the next lecture (04/04/2022), we'll see how this augmenting path may be easily transformed into an M-augmenting path in the original graph G (by "unshrinking" the relevant blossoms step-by-step), and we'll proceed to formalize the algorithm.