filmov
tv
Find the Area of the Green Rectangle | Step-by-Step Explanation
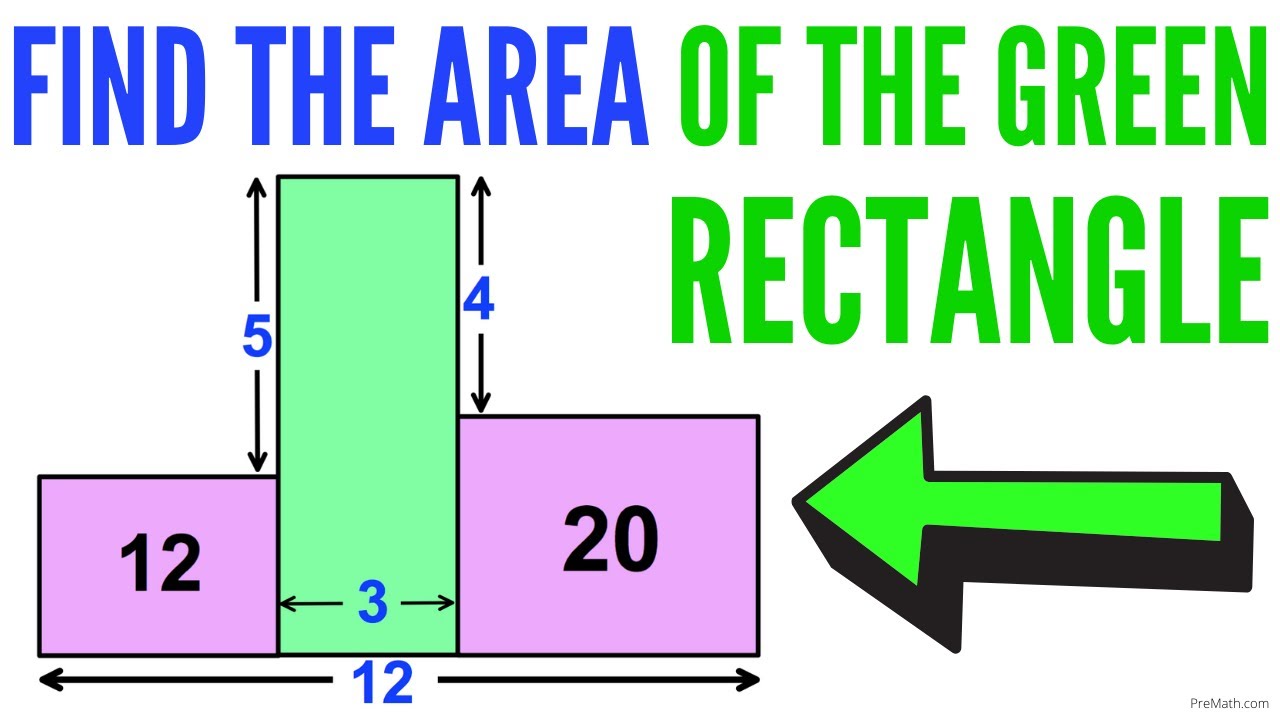
Показать описание
Math Antics - Area
Find the Area Challenge
Finding the Area of a Composite Figure | Area of Composite Rectangles
Find the area of the circle | Sweden Math Olympiad Geometry Problem
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Area for Kids
How to Find the Area of a Rectangle | Math with Mr. J
Find the Total Surface Area of a Cone in 60 Seconds | Sangram sir| #shortsvideo
Area of square | How to find area of the square #shorts
How to Find the Area of a Circle | Area of a Circle Step by Step
Easy Way To Find The Area Of A Circle! #Shorts
How to Find the Area of a Square | Math with Mr. J
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Area of rectangle | How to find area of a rectangle #shorts
How to Find the Area of Rectangles and Squares | Math with Mr. J
How to Find the Surface Area of a Rectangular Prism | Math with Mr. J
Find the Area of an Equilateral Triangle
Can you find Perimeter and Area of the right triangle? | (Solve) | #math #maths | #geometry
Can you calculate area of the Trapezoid? | (Triangles) | #math #maths | #geometry
How to Find the Area of a Composite Shape | L-Shaped Example | Math with Mr. J
How to Find the Area and Perimeter of a Triangle | Math with Mr. J
Math Antics - Circles, Circumference And Area
Plus Two Mathematics | Application Of Integrals In 25 Minutes | Xylem Plus Two
Комментарии
 0:10:26
0:10:26
 0:04:33
0:04:33
 0:07:14
0:07:14
 0:15:51
0:15:51
 0:20:35
0:20:35
 0:22:10
0:22:10
 0:08:58
0:08:58
 0:04:43
0:04:43
 0:01:01
0:01:01
 0:00:30
0:00:30
 0:06:39
0:06:39
 0:00:30
0:00:30
 0:02:48
0:02:48
 0:06:37
0:06:37
 0:00:30
0:00:30
 0:06:57
0:06:57
 0:04:57
0:04:57
 0:00:47
0:00:47
 0:09:58
0:09:58
 0:11:16
0:11:16
 0:05:21
0:05:21
 0:05:48
0:05:48
 0:07:56
0:07:56
 0:26:33
0:26:33