filmov
tv
Olympiad Challenge | AIME 2000 Problem | Math Olympiad Preparation | PRMO | No Calculator | A-Maths
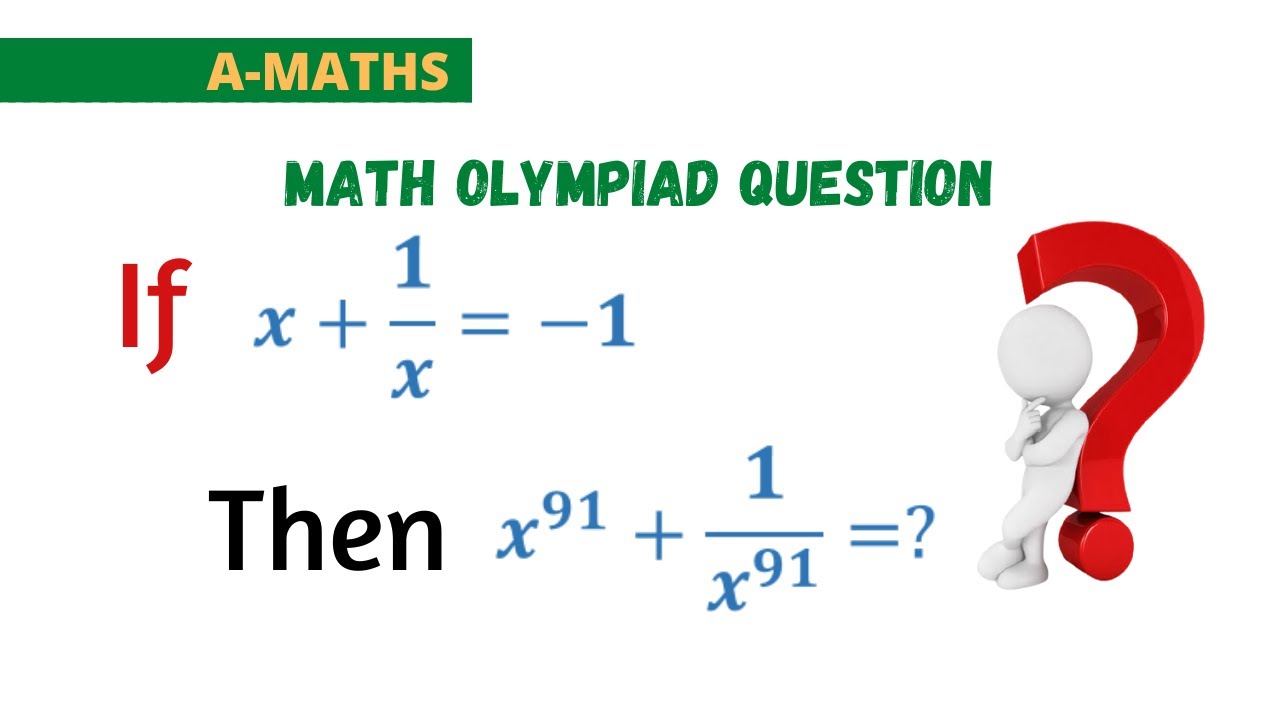
Показать описание
Olympiad Challenge | AIME 2000 Problem | Math Olympiad Preparation | PRMO | No Calculator | A-Maths
"This tutorial demonstrates "How to solve a Nonlinear equation for Pre Regional Mathematics Olympiad, a junior math olympiad problem with solution"
I will share tips and Tricks to solve an olympiad math question in a simple way and you will be able to solve a math olympiad problem fast after this math olympiad training.
"A-Maths" is dedicated to helping middle school, high school, and community college students who need to learn algebra and calculus. Topics include how to solve linear equations, quadratic equations, square root equations, rational equations, exponential equations, logarithmic equations, and more, factoring techniques, derivatives, chain rule, integration, by parts method and techniques belongs to math olympaid.
#amaths #challengingmathproblems #matholympiad #matholympics #radical #olympics #mathematicalolympiad
"This tutorial demonstrates "How to solve a Nonlinear equation for Pre Regional Mathematics Olympiad, a junior math olympiad problem with solution"
I will share tips and Tricks to solve an olympiad math question in a simple way and you will be able to solve a math olympiad problem fast after this math olympiad training.
"A-Maths" is dedicated to helping middle school, high school, and community college students who need to learn algebra and calculus. Topics include how to solve linear equations, quadratic equations, square root equations, rational equations, exponential equations, logarithmic equations, and more, factoring techniques, derivatives, chain rule, integration, by parts method and techniques belongs to math olympaid.
#amaths #challengingmathproblems #matholympiad #matholympics #radical #olympics #mathematicalolympiad
Olympiad Challenge | AIME 2000 Problem | Math Olympiad Preparation | PRMO | No Calculator | A-Maths
Olympiad Challenge | AIME 2000 Problem | Math Olympiad Preparation | Believe In Algebra | A-Maths
Olympiad Challenge | AIME 2000 Problem | Math Olympiad Preparation | PRMO | Nonlinear Log Equation
Solving an AIME problem in 1 Minute | AIME 2000 Problem 7
Putin vs Zelensky playing Piano
LeBron has spotted a fan 👀 #shorts
Putin flirts, Putin sigma rule, Putin body language #sigma #confidence #bodylanguage #putin #shorts
2000 AIME II Problem #7 A Challenging Combinatorics Question!
AIME 2000 | Algebra | American Math Olympiad | AAKRITI EDUCATIONS
'I'm A Dolphin': Amy and Tammy Go Swimming! | 1000-lb Sisters
I Blinked and This Happened
Therians are still human, you can’t hunt us 💀 #therian #quadrobics #fox #alterhuman #furry
Can anyone match Henry's skills?! 😭
The highest IQ ever 😲
PRMO 1| AIME 2000 Problem | SAT Math| IMO | Math Olympiad Preparation | Believe In Algebra | A-Maths
Marine Le Pen sur la chanteuse Aya Nakamura.
PRMO | AIME 2000 Problem | SAT Math| IMO | Math Olympiad Preparation | Believe In Algebra | A-Maths
Olympiad level counting (Generating functions)
Beyoncé as Blue Ivy reveals New York on Renaissance Tour Metlife stage 🥹💞
Kylian Mbappé collège. C’est vraiment lui ? #football #college #kylianmbappe #mbappe #humour #shorts...
President KAGAME❤️FIRST LADY
PERFECT archery shot with her compound bow and arrow
Challenging Olympiad Math Question | AMC 8 10 12 A B AIME I II 2022 2023 BMO Round 1 2 UKMT
Une équipe bien aggressive !🤣 #om #shortfootball #soccer #football #guendouzi #challenge
Комментарии
 0:05:40
0:05:40
 0:14:28
0:14:28
 0:03:10
0:03:10
 0:01:20
0:01:20
 0:00:28
0:00:28
 0:00:28
0:00:28
 0:00:20
0:00:20
 0:05:12
0:05:12
 0:03:20
0:03:20
 0:06:38
0:06:38
 0:00:20
0:00:20
 0:00:09
0:00:09
 0:00:22
0:00:22
 0:00:56
0:00:56
 0:03:29
0:03:29
 0:00:55
0:00:55
 0:03:43
0:03:43
 0:34:36
0:34:36
 0:00:24
0:00:24
 0:00:18
0:00:18
 0:00:13
0:00:13
 0:00:08
0:00:08
 0:02:43
0:02:43
 0:00:27
0:00:27