filmov
tv
Midpoints and bisectors | Universal Hyperbolic Geometry 16 | NJ Wildberger
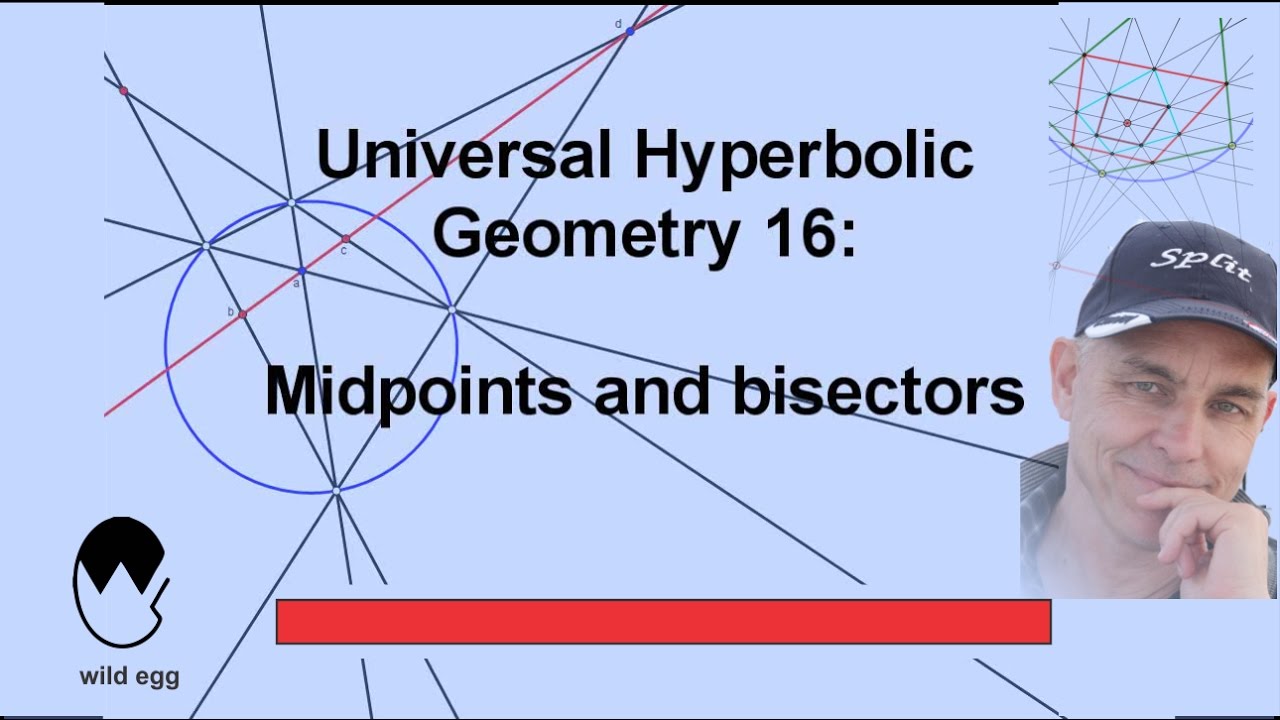
Показать описание
Midpoints of sides may be defined in terms of reflections in points in hyperbolic geometry. Reflections are defined by 2x2 trace zero matrices associated to points. The case of a reflection in a null point is somewhat special. The crucial property of reflection is that it preserves perpendicularity, which then implies that reflections send lines to lines. Midpoints of a side bc can be constructed with a straightedge when they exist, and in general there are two of them! This is a big difference with Euclidean geometry. Bisectors of vertices are defined by duality.
Video Content:
00:00 Introduction
3:28 Definition of reflection of a general point
7:32 Null reflection theorem
9:29 Matrix perpendicularity theorem
14:29 Reflection (preserves) perpendicularity theorem
18:11 Reflection (preserves) lines theorem
21:24 Midpoint between 2 points
24:25 Geometrical construction of midpoints 1a)
28:59 Geometrical construction of midpoints 1b)
31:41 Geometrical construction of midpoints 2
33:34 Not all sides have midpoints; side/vertex midpoints/bisectors
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
Video Content:
00:00 Introduction
3:28 Definition of reflection of a general point
7:32 Null reflection theorem
9:29 Matrix perpendicularity theorem
14:29 Reflection (preserves) perpendicularity theorem
18:11 Reflection (preserves) lines theorem
21:24 Midpoint between 2 points
24:25 Geometrical construction of midpoints 1a)
28:59 Geometrical construction of midpoints 1b)
31:41 Geometrical construction of midpoints 2
33:34 Not all sides have midpoints; side/vertex midpoints/bisectors
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
Комментарии
 0:36:41
0:36:41
 0:18:04
0:18:04
 0:06:48
0:06:48
 0:11:08
0:11:08
 0:13:51
0:13:51
 0:04:53
0:04:53
 0:14:20
0:14:20
 0:38:06
0:38:06
 0:34:09
0:34:09
 0:01:22
0:01:22
 0:12:21
0:12:21
 0:13:25
0:13:25
 0:05:56
0:05:56
 0:30:48
0:30:48
 0:06:16
0:06:16
 0:05:12
0:05:12
 0:00:13
0:00:13
 0:56:03
0:56:03
 0:22:26
0:22:26
 0:09:26
0:09:26
 0:02:33
0:02:33
 0:29:49
0:29:49
 0:32:46
0:32:46
 0:10:36
0:10:36