filmov
tv
Medians, midlines, centroids and circumcenters | Universal Hyperbolic Geometry 17 | NJ Wildberger

Показать описание
Here we introduce basic aspects of triangle geometry into the superior framework of universal hyperbolic geometry, a purely algebraic setting valid over the rational numbers. We begin by reviewing the centroid and circumcenter in the Euclidean setting. In the hyperbolic plane, midpoints of a side don't always exist. If we consider a triangle in which each side has midpoints, there are then 6 medians, and their dual lines, called midlines here, although they play the role of perpendicular bisectors. The medians meet in 4 centroids. The midlines meet in 4 circumcenters.
There are some remarkable connections between centroids and circumcenters, culminating in the z point of the triangle. Remarkably it lies on the ortho-axis, and together with the base center, orthocenter and orthostar, forms a harmonic range of points. THANKS to EmptySpaceEnterprise for help with Video Contents.
Video Content:
00:00 Introduction
04:25 Euler line
06:06 Midlines of a side
9:47 # of midpoints of a triangle; duals of midpoints
18:27 Meets of medians theorem
20:14 construction of meets of midlines (circumcenters)
25:01 Centroid circumcenter correspondence theorem
29:06 Z-point ortho-axis theorem
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
There are some remarkable connections between centroids and circumcenters, culminating in the z point of the triangle. Remarkably it lies on the ortho-axis, and together with the base center, orthocenter and orthostar, forms a harmonic range of points. THANKS to EmptySpaceEnterprise for help with Video Contents.
Video Content:
00:00 Introduction
04:25 Euler line
06:06 Midlines of a side
9:47 # of midpoints of a triangle; duals of midpoints
18:27 Meets of medians theorem
20:14 construction of meets of midlines (circumcenters)
25:01 Centroid circumcenter correspondence theorem
29:06 Z-point ortho-axis theorem
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
Комментарии
 0:34:09
0:34:09
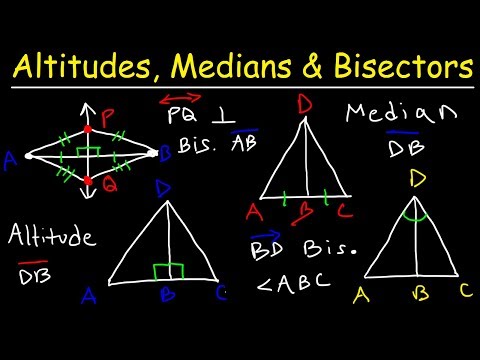 0:10:18
0:10:18
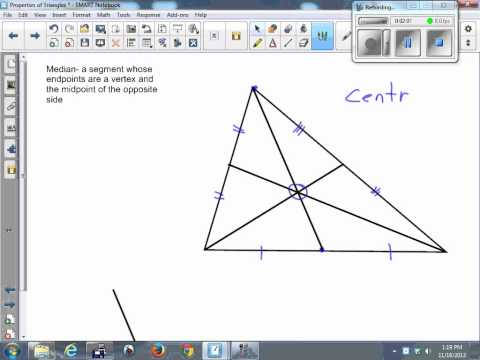 0:03:28
0:03:28
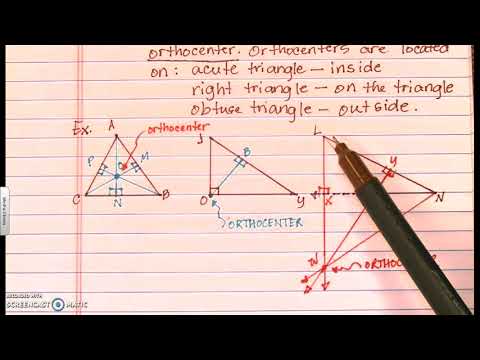 0:10:54
0:10:54
 0:05:37
0:05:37
 0:11:45
0:11:45
 0:16:59
0:16:59
 0:04:01
0:04:01
 0:03:01
0:03:01
 0:29:49
0:29:49
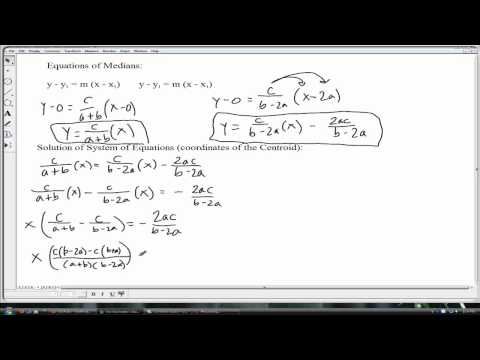 0:09:35
0:09:35
 0:00:44
0:00:44
 0:40:48
0:40:48
 0:00:11
0:00:11
 0:00:11
0:00:11
 0:09:26
0:09:26
 0:12:55
0:12:55
 0:09:04
0:09:04
 0:04:49
0:04:49
 0:04:53
0:04:53
 0:11:33
0:11:33
 0:16:18
0:16:18
 0:00:11
0:00:11
 0:00:11
0:00:11