Factoring a perfect square trinomial with fractions, boo ex 31, x^2 + x + 1/4

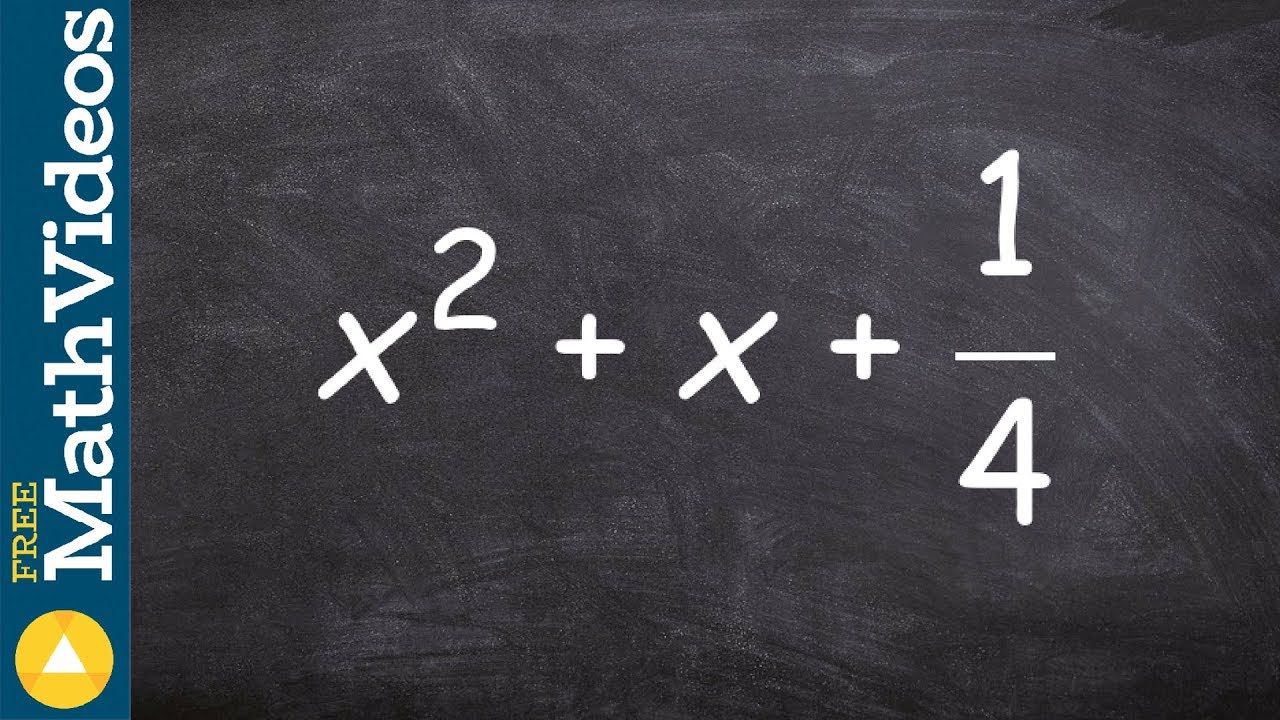
Показать описание

👉Learn how to factor perfect square trinomials. Perfect square trinomials are formed when binomials are multiplied by themselves. To factor an algebraic expression means to break it up into expressions that can be multiplied together to get the original expression.

Factoring perfect square trinomial goes through the same proces of factoring quadratic trinomials. To factor a perfect square trinomial, we find two expressions which when multiplied together gives the product of the constant term (the term with no variable) and the term with the squared variable and when the two expressions are added gives the term whose variable has no power. These two expressions obtained are used to replace the term whose variable has no power. The result is then factored by grouping them and factoring out the GCD.

If the coefficient of the squared variable is 1, all we need to do is to find two numbers which when multiplied together gives the constant term (the term with no variable) and when the two numbers are added gives the coefficient of the the term whose variable has no power. These two numbers are written with the variable in two separate parenthesis.

Organized Videos:
✅Factor Quadratic Expressions
✅Factor Quadratic Expressions | Learn About
✅Factor Quadratic Expressions | GCF
✅Factor Quadratic Expressions | x^2+bx+c
✅Factor Quadratic Expressions | x^2+bx+C
✅Factor Quadratic Expressions | Difference of Two Squares
✅Factor Quadratic Expressions | Perfect Square
✅Factor Quadratic Expressions | ax^2+bx+c

Connect with me:

#quadratics #factoring #brianmclogan

Рекомендации по теме

Комментарии

Brilliant video. I've been working on squsres of binomials with fractions gor over a day and I have just nailed it. 👍👍

ikemuoma

Following another video of his, I first factored out 1/4 (i.e., multiplied all the terms by 4) and then factored the rest, resulting in (1/4)(2x + 1)².

KW-gbcd