filmov
tv
Find The Yellow Shaded Area | Math Olympiad | A nice Geometry Problem

Показать описание
Find The Yellow Shaded Area | Math Olympiad | A nice Geometry Problem
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Arichai Vattanapat
Sambasivam Sathyamoorthy
Abebe Melesse
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Arichai Vattanapat
Sambasivam Sathyamoorthy
Abebe Melesse
Can you find area of the Yellow shaded region? | (Circles) | #math #maths | #geometry
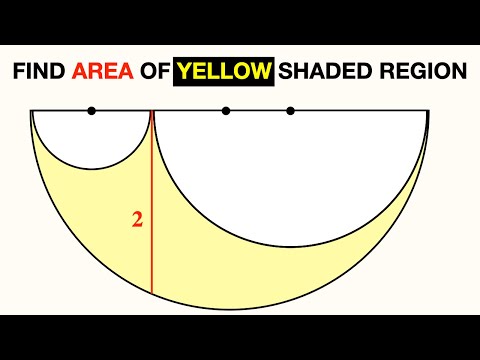
Can you find area of the Yellow shaded region? | (Rectangle) | #math #maths | #geometry
Find Yellow Shaded Area - Challenging Olympiad Question | Important Geometry Skills Explained
Can you find the area of the Yellow shaded region? | #math #maths
Can you find area of the Yellow shaded region? | (Quarter Circle) | #math #maths | #geometry
Find area of Yellow shaded region inscribed in a right triangle | Step-by-step tutorial
Can you find area of the Yellow shaded region? | (Square and Circle) | #math #maths | #geometry
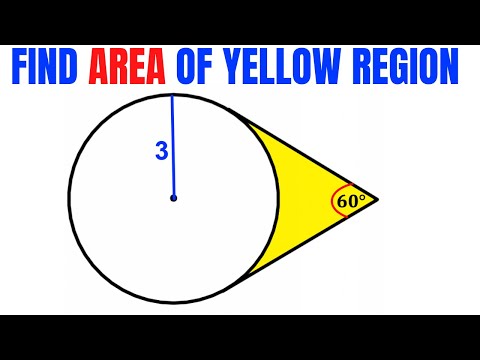
Calculate area of the Yellow shaded region | Radius is 3 | Important Geometry skills are explained
Find out how to become an American Home Buyer on Houston Happens!
Can you find the area of the Yellow shaded region? | AB=8 | (Nine identical circles) | #math #maths
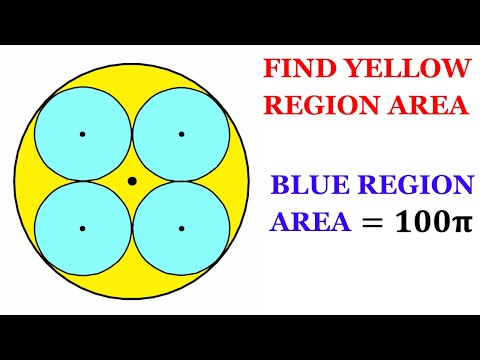
Math Olympiad | Can you find the Yellow shaded region area? | (4 identical circles) | #math #maths
Can you find area of the Yellow shaded region? | (Quarter circle) | #math #maths | #geometry
How to Find Yellow Shaded Area in the Circle | Geometry | Math
Can you find area of the Yellow shaded Quarter circle? | (Chords) | #math #maths | #geometry
Can you find area of the Yellow shaded Square? | (Triangle) | #math #maths | #geometry
Calculate area of Yellow shaded region | Radius of the big circle is 12 | Important skills explained
Math Olympiad | Find area of the Yellow shaded region? | (Quarter circles and square) | #math #maths
Can you find area of the Yellow shaded region? | (Step-by-step explanation) | #math #maths
Find the Area of Shaded Region in Yellow | Maths | Circles and Triangle | IMO Olympiad
Find Area of the Yellow Shaded Triangle | Important Geometry & Algebra Skills Explained
Can you find area of the Yellow shaded Triangle? | (Trapezoid) | #math #maths | #geometry
Calculate area of the Yellow shaded circle | Semicircle | (Important Geometry skills explained)
Can you find area of the Yellow shaded region? | (Intersecting Chords) | #math #maths | #geometry
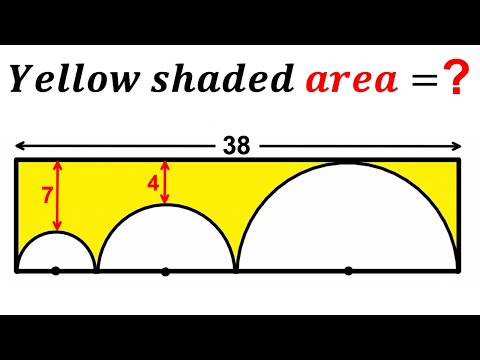
Can you find area of the Yellow shaded region? | (Rectangle) | #math #maths | #geometry
Комментарии
 0:08:58
0:08:58
 0:09:59
0:09:59
 0:07:41
0:07:41
 0:10:21
0:10:21
 0:12:43
0:12:43
 0:11:53
0:11:53
 0:10:55
0:10:55
 0:10:29
0:10:29
 0:56:32
0:56:32
 0:09:05
0:09:05
 0:10:31
0:10:31
 0:08:38
0:08:38
 0:04:33
0:04:33
 0:08:06
0:08:06
 0:08:42
0:08:42
 0:09:31
0:09:31
 0:12:09
0:12:09
 0:12:14
0:12:14
 0:03:12
0:03:12
 0:05:06
0:05:06
 0:12:39
0:12:39
 0:12:40
0:12:40
 0:12:45
0:12:45
 0:09:18
0:09:18