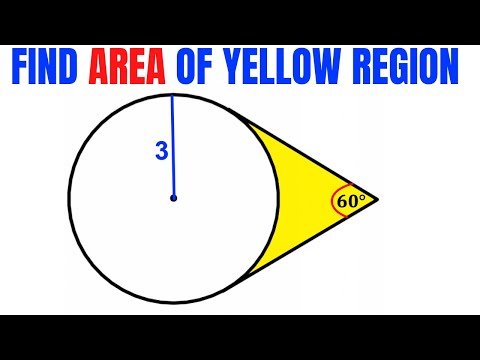
Calculate area of the Yellow shaded region | Radius is 3 | Important Geometry skills are explained

Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy way. Learn how to prepare for Math Olympiad fast!

Need help with solving this Math Olympiad Question? You're in the right place!

I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at

Calculate area of the Yellow shaded region | Radius is 3 | Important Geometry skills are explained

Olympiad Mathematical Question! | Learn Tips how to solve Olympiad Question without hassle and anxiety!

#CalculateAreaOfYellowShadedRegion #CalculateArea #AreaOfSector #AreaOfTriangle#GeometryMath #PythagoreanTheorem #PerpendicularBisectorTheorem
#MathOlympiad #ThalesTheorem #RightTriangle #RightTriangles #CongruentTriangles
#OlympiadMathematicalQuestion #HowToSolveOlympiadQuestion #MathOlympiadQuestion #MathOlympiadQuestions #OlympiadQuestion #Olympiad #AlgebraReview #Algebra #Mathematics #Math #Maths #MathOlympiad #HarvardAdmissionQuestion
#MathOlympiadPreparation #LearntipstosolveOlympiadMathQuestionfast #OlympiadMathematicsCompetition #MathOlympics #CollegeEntranceExam
#blackpenredpen #MathOlympiadTraining #Olympiad Question #GeometrySkills #GeometryFormulas #Angles #Height
#MathematicalOlympiad #OlympiadMathematics #CompetitiveExams #CompetitiveExam

How to solve Olympiad Mathematical Question
How to prepare for Math Olympiad
How to Solve Olympiad Question
How to Solve international math olympiad questions
international math olympiad questions and solutions
international math olympiad questions and answers
olympiad mathematics competition
blackpenredpen
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
Po-Shen Loh and Lex Fridman
Number Theory
There is a ridiculously easy way to solve this Olympiad qualifier problem
This U.S. Olympiad Coach Has a Unique Approach to Math
The Map of Mathematics
mathcounts
math at work
Pre Math
Olympiad Mathematics
Two Methods to Solve System of Exponential of Equations
Olympiad Question
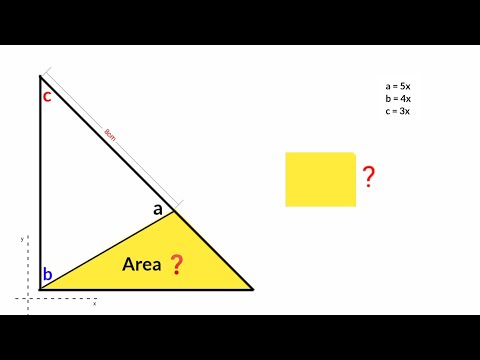
Find Area of the Shaded Triangle in a Rectangle
Geometry
Geometry math
Geometry skills
Right triangles
imo
Competitive Exams
Competitive Exam
Calculate the Radius
Area of sector
Pythagorean Theorem
Equilateral triangle
Right triangles
Circle
Square
Area of triangle
Area of circle

Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.

[ybodoN]

Alternatively, just subtract the area of the circular segment AB from the area of the equilateral triangle ABC.
(the area of the circle minus the area of the triangle ABC is three times the area of the circular segment AB)

[Dimitar_Stoyanov_]

Exactly the way I would solve this! Great! 👍👌

[zawatsky]

Из двух треугольников можно сложить прямоугольник, потому площадь четырёхугольника - произведение большей и меньшей сторон. Можно было обойтись без промежуточных вычислений.

[Reddogovereasy]

Thank you, very well presented. Please keep these problems coming.

[spiderjump]

area of OACB= 1/2x BCXOB X2

triangle OBC is 30 60 rt triangle hence BC = square root of 6x6 --3x3)
=3 x sqroot of 3

area of OACB= 9x sqroot of 3
area of sector 0AB =120/360 XPI X3X3
=3PI

hence shaded area = 9x sqroot3 -- 3 pi

[EnnioPiovesan]

Consider the extension of CO beyond O until it meets the circle at H and through H draw the tangent to the circle. This intersects the line CB at Q and the line CA at P.
Thus we have an equilateral triangle CPQ circumscribed to the circumference whose side is, for example, l=2BC.
Now BC is the major leg of the right-angled triangle OBC which has angles of 30° and 60° and therefore BC=OB √3.
Consequently l=6 √3.
The area of ​​the equilateral triangle CPQ is therefore [CPQ]=(l²/4)√3=3·3²·√3.

The yellow area is one third of the difference between the area of ​​the triangle CQP and that of the circumference and therefore its value is:
(1/3)[(3·3²·√3)-9π]=9√3-3π.

[DaysInApril]

AKA - how to calculate the area of a traverse with a horizontal curve.. useful for EIT and LSIT exams

[jbreezy]

Great skill for approximating the storm-relative helicity in tornado forecasting

[quigonkenny]

By Two Tangent Theorem, BC = AC and by Circle Theorem ∠OBC and ∠OAC are both 90°. As OB = OC, ∆OBC and ∆OAC are congruent. By observation, ∠OCB and ∠OCA are both (1/2)60° = 30°. As OB = 3:

Triangle ∆OBC
O/H = sin θ
3/OC = sin 30° = 1/2
OC = 3(2) = 6

A/H = cos θ
BC/6 = (√3)/2
BC = (6√3)/2 = 3√3

By obaervation, yellow area is equal to sum of ∆OBC and ∆OAC minus Sector BOA. ∠BOA = 360-2(90)-60 = 360-240 = 120°

A = bh/2 + bh/2 - (θ/360)πr²
A = 2[3(3√3)/2] - (120/360)π(3²)
A = 9√3 - (9/3)π = 9√3 - 3π ≈ 6.16

[vidyadharjoshi]

Draw Line ODC where D is on the circle. OD = DC = 3. OC = 6, BC = sqrt27.
Area of sector OAB = (1/3)*Pi*9. Area of OACB = 2*(1/2)*3*sqrt27. Yellow Area = 3sqrt27 - 3Pi = 6.16

[johnplong]

There is so much geometry that I have forgotten . This is not a real hard problem just a lot of steps You just have to grind it out I haven’t done this in over 47!years I know for a fact I did similar problems like this at one time I have absolutely no problem following what is being done Nice job in explaining how to do this problem

[chrisc]

Very nice problem. I drew a line from point B to A, then used this to form a square. then used pythagoras to calculate the side of the square. After, calculate normally by taking circle - area of square /4. Then triangle-that = the answer

[vara]

Sir to calculate AC which is equal to BC, we can use trigonometry solution. Tan 60 deg= AC/OA.
Tan 60= AC/3
Sqrt of 3= AC/3
Therefore AC= 3*Sqrt of 3.
PS: there is no squareroot symbol in my phone.
And we can proceed with manner. you have shown us.

[marioalb]

Yellow area = Area of equilateral triangle - Area of circular segment

Area of equilateral triangle = b x h / 2
b = 2 ( R cos30°)
h = b. cos 30°
Area et = 5, 196 x 4, 5 / 2
Área et = 11, 69 cm²

Área of circular segment =
= ½ R² ( α - sinα )
= ½ 3² (120° - sin 120°)
Área cs = 5, 528 cm²

Área = Área et - Área cs
Area = 11, 69 - 5, 528
Area = 6, 16 cm² ( Solved √ )

[marioalb]

Yellow area = Area of quadrilateral - Area of circular sector

Area of quadrilateral =
2 x Area of right triangle

Area right triangle = ½ b x h
b = 2 R = 6 cm
h = R cos 30° = 2, 598 cm

Area quad. = 6 x 2, 598
Área quad = 15, 588 cm²

Área of circular sector =
=π R² ( 120/360 )
= π 3² /3
Área cs = 9.425 cm²

Área = Área quad - Área cs
Area = 15, 588 - 9, 425
Area = 6, 16 cm² ( Solved √ )

[haticealbayrak]

it doesn't matter where edges of 60° vectors touch perimeter of circle it is always is the area of 60°triangle whose edges are at the lenght of diameter of circle minus half the area of circle at given radius. you can prove thhis by dividing the diamond shape 2 equal triangles drawing a line from center of circle to vectoral origin .

[yvessioui]

What that had me a little excited would have been tosee the construction of a general way to find such area whatever the outside angle could be. 30° being a specific case of that general 'formula'. The thing here being able to find as a general case with no trig or integration if possible.

[kennethstevenson]

I got the correct answer on the first try without additional help.

[zoltanpetofi]

hmmm.... much faster to calculate area of OACB is multiply diagonals, then devide by two so 6 * 3*sqrt3 / 2 = 9 * sqrt3.
But...
Fastest way to use general formula, in special case of 60 degrees: area = r^2(sqrt3 - pi/3)

[solimana-soli]

known that the triangle ABC is equilateral, I have calculated the area of the quadrilateral ACBO as the product of the diagonals divided by 2