filmov
tv
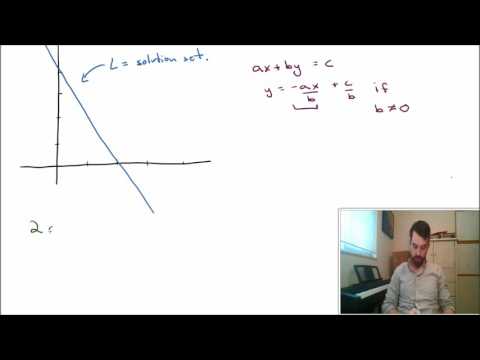
Geometric meaning of solutions to a linear equation in 2D

Показать описание
Learning Objectives:
1) Sketch the solutions to a linear equation in 2D
2) Determine whether a linear equation has 0 or infinitely many solutions in 2D
This video is part of a Linear Algebra course taught at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
1) Sketch the solutions to a linear equation in 2D
2) Determine whether a linear equation has 0 or infinitely many solutions in 2D
This video is part of a Linear Algebra course taught at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Geometric meaning of solutions to a linear equation in 2D
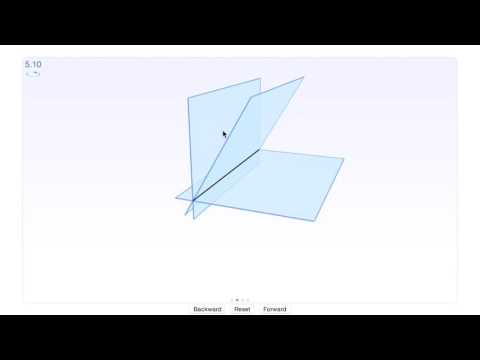
Geometric meaning of a linear system in 2D
The Geometric Meaning of Differential Equations // Slope Fields, Integral Curves & Isoclines
Geometric View on Solutions to Ax=b and Ax=0.
Geometric Meaning of the Number of Solutions to the Linear System
The geometric interpretation of systems of linear equations in 2 & 3 dimensions
Cracking matrix calculation : Geometric interpretation of matrices
Interpretation of solutions to a system of equations in 3D
Geometric Interpretation of Linear Systems of Equations
How to Find the Geometric Means? Geometric Sequence - Grade 10 Math
How To Calculate The Geometric Mean
Imaginary Numbers Are Real [Part 1: Introduction]
Geometric interpretation of simultaneous linear equations 2D
Geometric Mean Class 10 #shorts
Arithmetic Mean, Geometric Mean, Weighted Mean, Harmonic Mean, Root Mean Square Formula - Statistics
Differential equations, a tourist's guide | DE1
Cramer's rule, explained geometrically | Chapter 12, Essence of linear algebra
Quadratic Equations - Geometrical Meaning
Missing Angles Geometry Problem | Tricky Math Question | JusticeTheTutor #maths #math #shorts
Thursday: 8M4TDL25 Geometric Interpretation of the Solutions of a Linear System
Geometrical meaning of solutions of pair of linear equations in two variables
One Solution, No Solution, or Infinitely Many Solutions - Consistent & Inconsistent Systems
8M4 L25 - Geometric Interpretation of the Solutions of a Linear System
Ordinary Differential Equations - Geometric Interpretation
Комментарии
 0:05:06
0:05:06
 0:04:15
0:04:15
 0:09:52
0:09:52
 0:06:21
0:06:21
 0:01:43
0:01:43
 0:06:33
0:06:33
 0:07:32
0:07:32
 0:03:23
0:03:23
 0:12:10
0:12:10
 0:08:05
0:08:05
 0:05:56
0:05:56
 0:05:47
0:05:47
 0:09:27
0:09:27
 0:00:47
0:00:47
 0:52:44
0:52:44
 0:27:16
0:27:16
 0:12:12
0:12:12
 0:04:20
0:04:20
 0:00:37
0:00:37
 0:07:39
0:07:39
 0:04:15
0:04:15
 0:07:30
0:07:30
 0:20:21
0:20:21
 0:20:56
0:20:56