filmov
tv
Tensors for Beginners 13: Tensor Product vs Kronecker Product
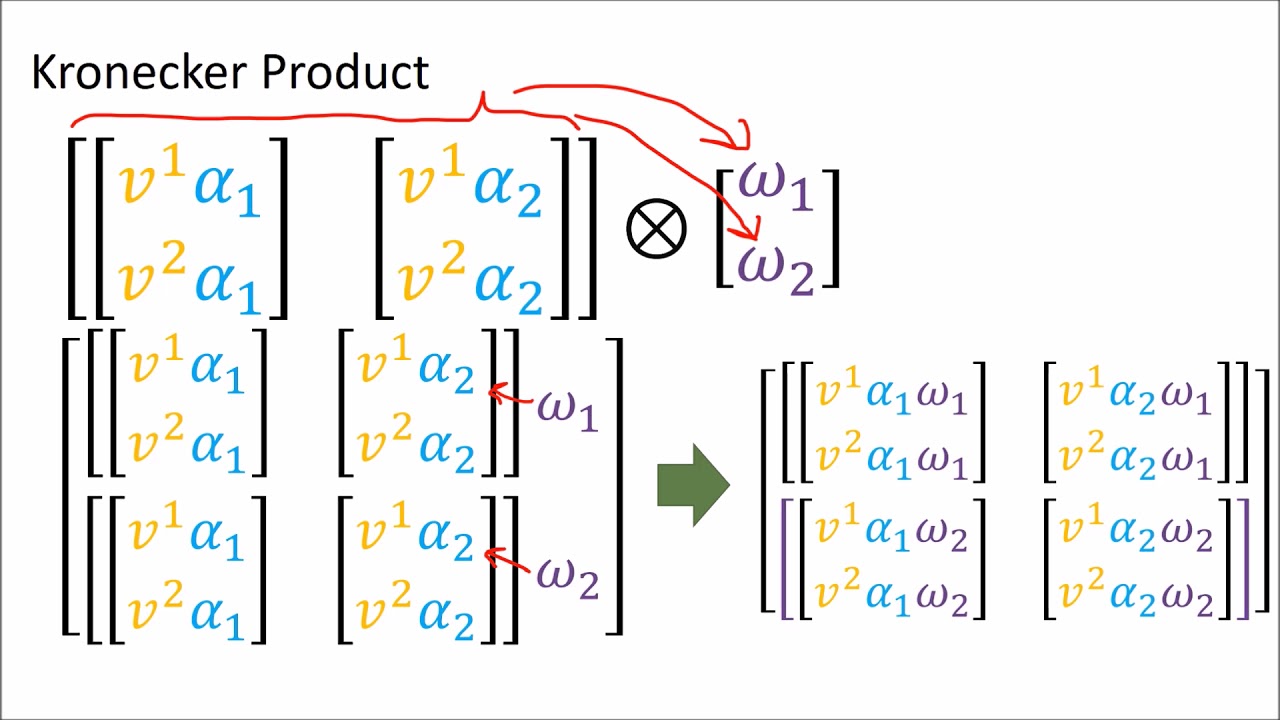
Показать описание
Tensors for Beginners 13: Tensor Product vs Kronecker Product
Tensors for Beginners 15: Tensor Product Spaces
Tensors for Beginners 0: Tensor Definition
Tensors for Beginners 9: The Metric Tensor
Tensors For Beginners (-1): Motivation
Tensors for Beginners 14: Tensors are general vector/covector combinations
Tensors for Beginners 12: Bilinear Forms are Covector-Covector pairs
Tensor Products are just Matrix Multiplication, Seriously.
What is Dirac Equation | Dirac Equation Explained | Dirac Equation for Beginners
Tensors for Beginners 5: Covector Components (Contains diagram error; see description)
Tensors for Beginners 2: Vector definition
Tensors for Beginners 3: Vector Transformation Rules
Tensors for Beginners 8: Linear Map Transformation Rules
Why are tensors EVERYWHERE? | Tensors for beginners #SoME
Tensors for Beginners 7: Linear Maps
A Concrete Introduction to Tensor Products
Tensor Calculus 13: Gradient vs 'd' operator (exterior derivative/differential)
Tensors for Beginners 6: Covector Transformation Rules
Tensors/tensor products demystified
TensorFlow Tutorial 02 - Tensor Basics - Beginner Course
The Metric Tensor - Tensors #13
Calculus 3: Tensors (13 of 45) What is the Inertia Tensor?
Demystifying The Metric Tensor in General Relativity
Tensor Calculus 0: Introduction
Комментарии
 0:04:47
0:04:47
 0:15:22
0:15:22
 0:09:57
0:09:57
 0:16:10
0:16:10
 0:06:26
0:06:26
 0:08:50
0:08:50
 0:07:28
0:07:28
 0:16:21
0:16:21
 1:00:19
1:00:19
 0:08:48
0:08:48
 0:09:17
0:09:17
 0:05:54
0:05:54
 0:11:35
0:11:35
 0:09:23
0:09:23
 0:12:05
0:12:05
 0:37:40
0:37:40
 0:19:07
0:19:07
 0:06:41
0:06:41
 1:04:15
1:04:15
 0:22:44
0:22:44
 0:11:14
0:11:14
 0:04:40
0:04:40
 0:14:29
0:14:29
 0:12:43
0:12:43