filmov
tv
Tensors for Beginners 12: Bilinear Forms are Covector-Covector pairs
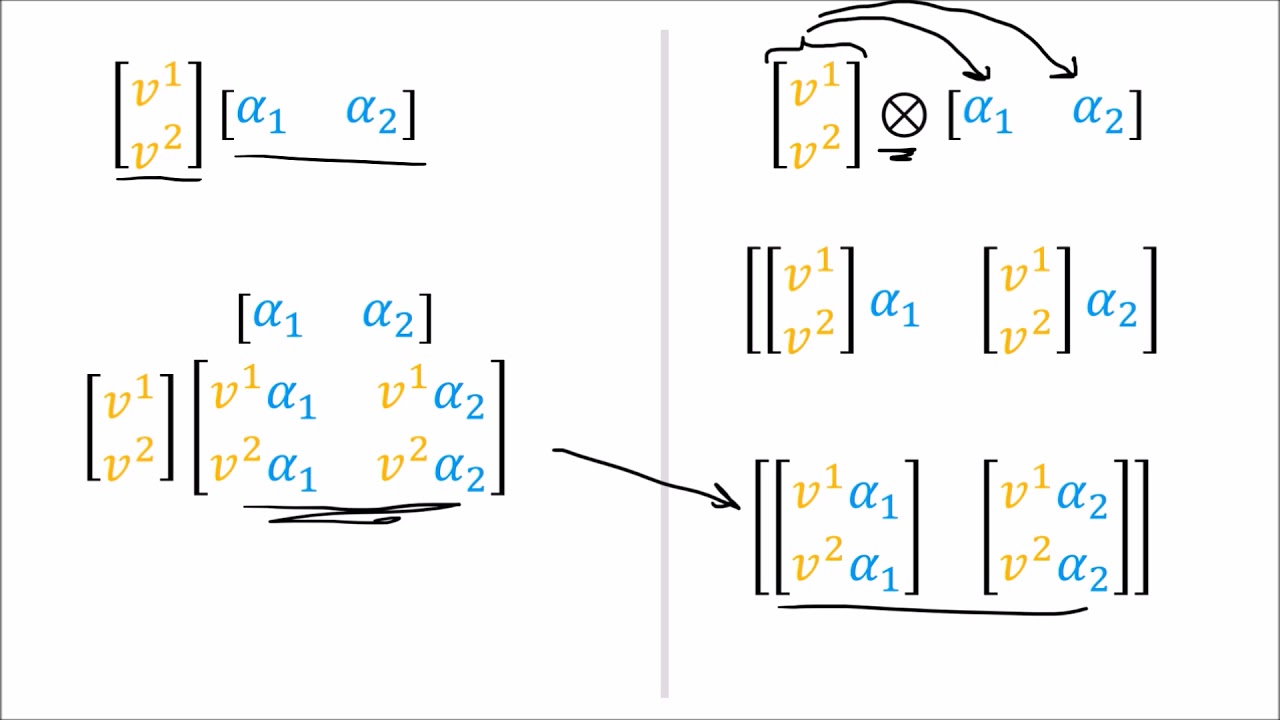
Показать описание
At 7:04 there are mistakes in the 3rd and 4th lines... Some of the B indexes are reversed.
So I got a new mic. It probably sounds like I'm 5 different people in this video because of the re-recordings I did. I hope it's not too distracting.
So I got a new mic. It probably sounds like I'm 5 different people in this video because of the re-recordings I did. I hope it's not too distracting.
Tensors for Beginners 12: Bilinear Forms are Covector-Covector pairs
Tensors for Beginners 10: Bilinear Forms
Tensors For Beginners (-1): Motivation
Tensors for Beginners 9: The Metric Tensor
Tensors for Beginners 8: Linear Map Transformation Rules
Tensors for Beginners 7: Linear Maps
Tensors for Beginners 15: Tensor Product Spaces
Tensors for Beginners 14: Tensors are general vector/covector combinations
Tensors for Beginners 0: Tensor Definition
Tensors for Beginners 11: Linear maps are Vector-Covector Pairs
Tensors for Beginners 5: Covector Components (Contains diagram error; see description)
Tensors for Beginners 13: Tensor Product vs Kronecker Product
Tensors for Beginners 4: What are Covectors?
Tensors for Beginners 2: Vector definition
Tensors for Beginners 6: Covector Transformation Rules
Tensors for Beginners 1 Forward and Backward Transformations contains error; read description!
Tensor Calculus 12: The Metric Tensor in Curved Spaces for Measuring Arc Length
Tensors for Beginners 16: Raising/Lowering Indexes (with motivation, sharp + flat operators)
Lecture 8 (Part 2): Bilinear maps, tensor products of 1-forms & vector fields
Advanced Calculus: dual space and bilinear mappings, tensor product of dual vectors, 10-16-23 part 2
Tensor Calculus 4: Derivatives are Vectors
Tensor Calculus 0: Introduction
Tensor Calculus 11: The Metric Tensor and Arc Lengths (flat space)
Tensor Calculus 7: Covector Field Components
Комментарии
 0:07:28
0:07:28
 0:09:52
0:09:52
 0:06:26
0:06:26
 0:16:10
0:16:10
 0:11:35
0:11:35
 0:12:05
0:12:05
 0:15:22
0:15:22
 0:08:50
0:08:50
 0:09:57
0:09:57
 0:12:07
0:12:07
 0:08:48
0:08:48
 0:04:47
0:04:47
 0:14:07
0:14:07
 0:09:17
0:09:17
 0:06:41
0:06:41
 0:09:09
0:09:09
 0:23:09
0:23:09
 0:15:44
0:15:44
 0:30:28
0:30:28
 0:57:57
0:57:57
 0:12:02
0:12:02
 0:12:43
0:12:43
 0:14:34
0:14:34
 0:14:19
0:14:19