filmov
tv
Calculating one BRUTAL Integral! Deriving Euler's Reflection Formula the RIDICULOUS way!
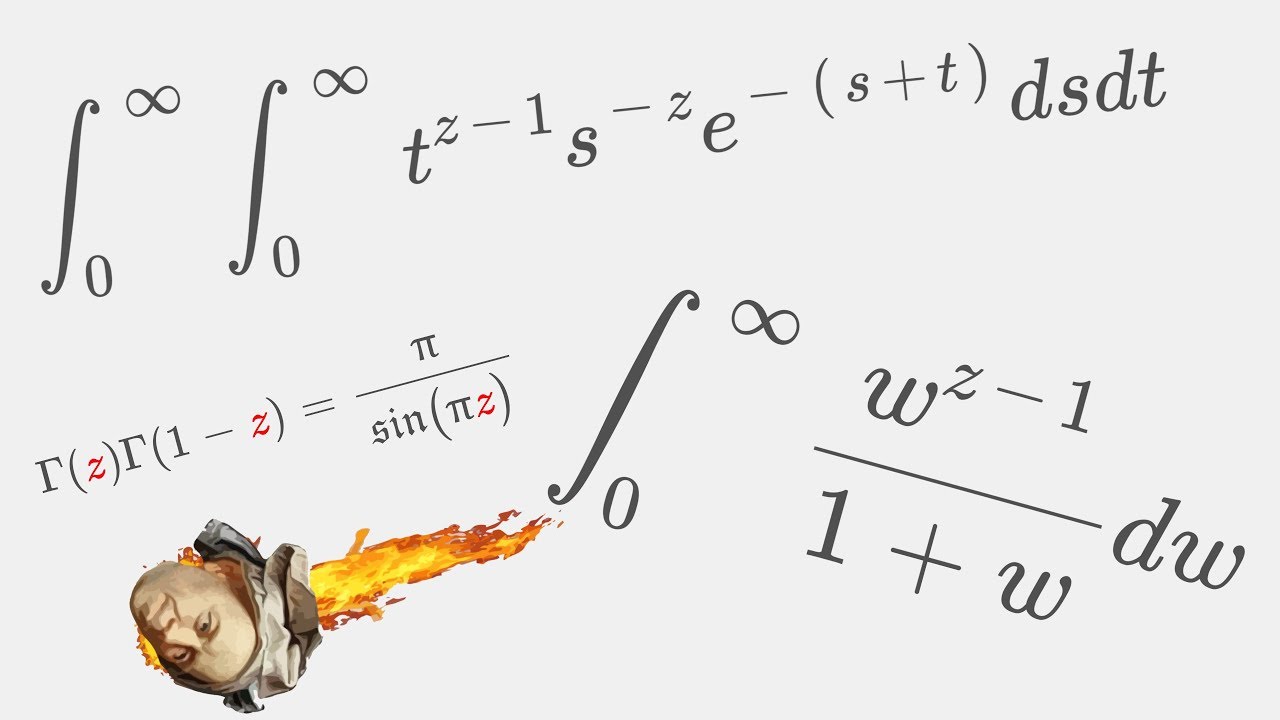
Показать описание
Help me create more free content! =)
Today we are going to go overbored! We are going to prove Euler's reflection formula today using the integral definition of the gamma function! What'S going to pop out is basically just a special case of the so-called Beta function. Surprisingly enough, we also get a single integral out of this whole ordeal, which is going o evaluate to teh pole expansion of the cosecans! =) Enjoy :)
Today we are going to go overbored! We are going to prove Euler's reflection formula today using the integral definition of the gamma function! What'S going to pop out is basically just a special case of the so-called Beta function. Surprisingly enough, we also get a single integral out of this whole ordeal, which is going o evaluate to teh pole expansion of the cosecans! =) Enjoy :)
Calculating one BRUTAL Integral! Deriving Euler's Reflection Formula the RIDICULOUS way!
how to solve these HARD integrals
So good!: ONE Integral, TWO Solutions! [ Desmos and WA Insights included ]
This is SERIESLY NUTS! Deriving the Sum of Reciprocals of the Odd Numbers Squared using INTEGRALS!
Eulerian Integral of the First Kind - Deriving the BETA FUNCTION! [ The non-trigonometric Version ]
ONE NEAT PROOF! Deriving the EULER DEFINITION of the Gamma Function!
Feynman would be proud. A Wonderful Generalized Integral.
A Class of very interesting Trigonometric Integrals!
Taylor series | Chapter 11, Essence of calculus
Evaluating an absolute Monster - Coxeter's Integral
A RIDICULOUS LIMIT! The Integral of cos(x) in its Riemann Sum form!
Legendre's Duplication Formula - A simple Proof!
Euler's Reflection Formula - Two very ELEGANT Proofs!
ζ(1) or The Harmonic Series Diverges - A flammable Proof [ + Python and Desmos ]
γ - A BRILLIANT Putnam Integral Journey - Analytic Number Theory at its finest
USSR vs USA Integration by Substitution
Edward Witten Epic Reply 🤣 Destroys String Theory Dissenters
Stand and Deliver (1988) - Tough Guys Don't Do Math Scene (2/9) | Movieclips
Gauss' Multiplication Formula - An Elementary Proof without Stirling!
This Result looks WAY TOO GOOD to be True! Transforming transcendental bois!
Non-Linear Numerical Methods Introduction | Numerical Methods
Natalia Tronko: Exact conservation laws for gyrokinetic Vlasov-Poisson equations
Lecture 4: Laplace's method
Numerical Integration Part 01
Комментарии
 0:24:05
0:24:05
 0:09:45
0:09:45
 0:22:25
0:22:25
 0:12:54
0:12:54
 0:17:28
0:17:28
 0:23:28
0:23:28
 0:13:55
0:13:55
 0:16:05
0:16:05
 0:22:20
0:22:20
 0:43:17
0:43:17
 0:19:36
0:19:36
 0:19:13
0:19:13
 0:13:55
0:13:55
 0:15:10
0:15:10
 0:23:23
0:23:23
 0:16:22
0:16:22
 0:01:42
0:01:42
 0:02:19
0:02:19
 0:29:19
0:29:19
 0:10:33
0:10:33
 0:03:41
0:03:41
 0:55:55
0:55:55
 1:14:53
1:14:53
 0:21:41
0:21:41