Algebra 96 Exponential Functions and Compound Interest

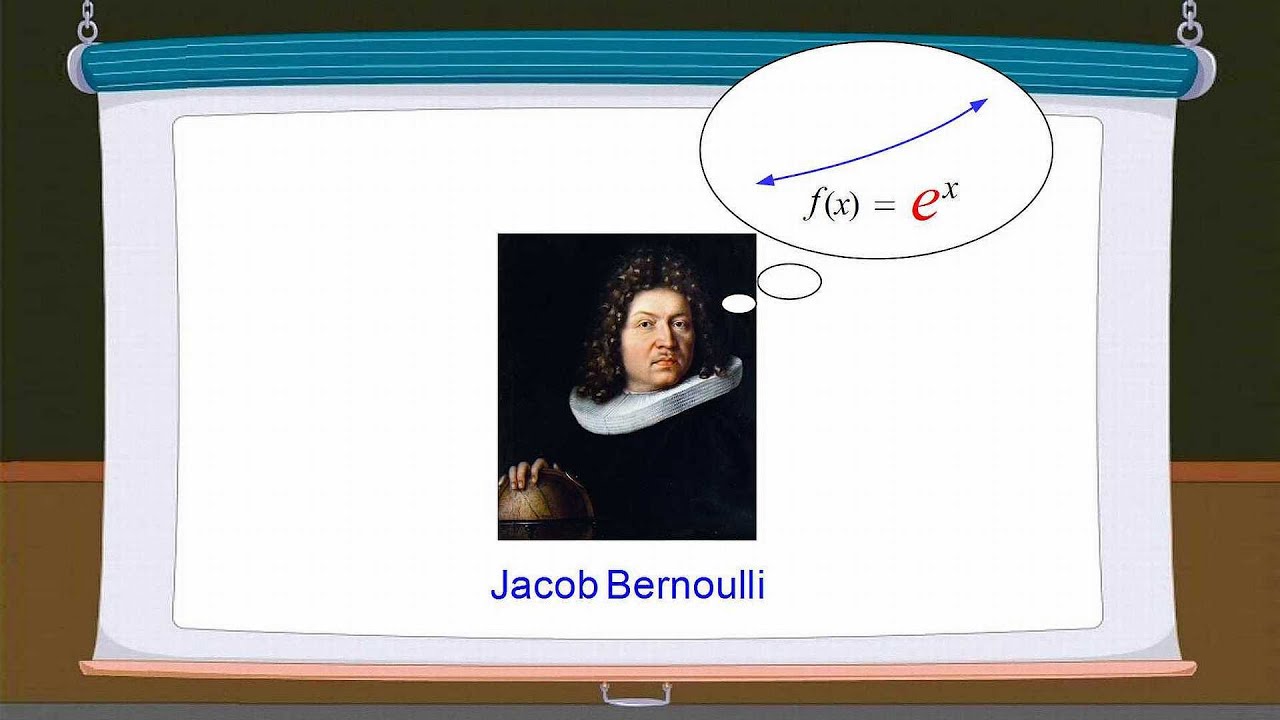
Exponential functions were first explored by the Swiss mathematician Jacob Bernoulli in sixteen-eighty-three, as a way of computing "continuous compound interest". When computing accruing interest and principal with continuous compounding, the compounding periods can be thought of as being infinitely short, with the increase in principal approaching the theoretical upper limit. In Bernoulli's quest to determine this upper limit, his research led to the development of the exponential function whose base is the constant "e", also known as "Euler's number". In this lecture, we use algebra to calculate compound interest with increasing shorter compounding periods, and show how this upper limit is approached.

[devrakkasi]

My dear respectable professor, it's good to see you. Thank you so much for giving us content. A lot of love from an Indian student.

[Groundsquirrel]

Wow! Thank you Steve Goldman and Mark Rodriguez for your time creating yet another great animated algebra lesson.

[dylanwishart]

Was literally JUST learning about Euler's number and how it was discovered from compound interest so I'm so glad there was a WhyU video to supplement my learning. Massive props to you guys for continuing this series for so many years. Eager for your next video!

[Prof_Michael]

It’s been a long time
Welcome back 😎😎😎

[Darkness-sgfx]

I wish I could live at least 1000 years so that I could possibly watch all the videos in this channel.

[hydrilara]

How many videos are left to complete this series according to your channel? I mean how many videos that you have to do to complete this algebra series?