filmov
tv
21. Stochastic Differential Equations

Показать описание
MIT 18.S096 Topics in Mathematics with Applications in Finance, Fall 2013
Instructor: Choongbum Lee
This lecture covers the topic of stochastic differential equations, linking probability theory with ordinary and partial differential equations.
00:21 - Stochastic Differential Equations
21:15 - Numerical methods
42:27 - Heat Equation
License: Creative Commons BY-NC-SA
Instructor: Choongbum Lee
This lecture covers the topic of stochastic differential equations, linking probability theory with ordinary and partial differential equations.
00:21 - Stochastic Differential Equations
21:15 - Numerical methods
42:27 - Heat Equation
License: Creative Commons BY-NC-SA
21. Stochastic Differential Equations
Ito's Lemma -- Some intuitive explanations on the solution of stochastic differential equations
Stochastic Calculus by Kamil Zajac
Robust and Stable Deep Learning Algorithms for Forward-Backward Stochastic Differential Equations
Stochastic Calculus Simplified: Intro to Stochastic Differential Equations - Integration Method
A system of stochastic differential equations in application
Introduction to Stochastic Calculus
C5.1.1 - Linear stochastic differential equations
Martin Hairer: Renormalization and Stochastic PDEs
Stochastic Processes I -- Lecture 21
stochastic differential equations
The Feynman-Kac formula, partial differential equations and Brownian motion [QCT21/22, Seminar #12]
Stochastic differential equations: Weak solution
Regularization by Noise in Stochastic Differential and Stochastic Partial Differential Equations
Numerical Solution for Stochastic Differential Equation
Functional Stochastic Differential Equations
Gunther Leobacher: Stochastic Differential Equations
Stochastic differential equations: Uniqueness
stochastic differential equation(SDE) SOLUTUON
C5.2.2 - General stochastic differential equations
Stochastic Differential Equation: Theory + Simulation Code in Fortran, Python: Euler-Maruyama Scheme
What does stochastic differential equation mean?
Score Based Generative Modeling through Stochastic Differential Equations Best Paper | ICLR 2021
Stochastic Differential Equations
Комментарии
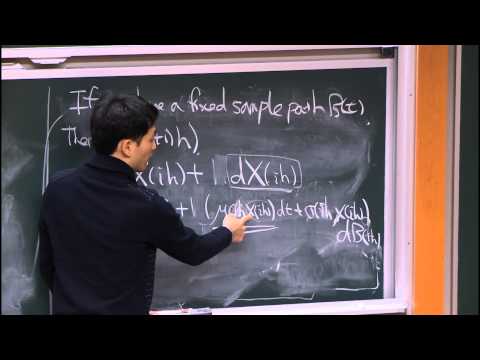 0:56:05
0:56:05
 0:25:29
0:25:29
 0:01:58
0:01:58
 0:22:00
0:22:00
 0:26:29
0:26:29
 0:14:28
0:14:28
 0:07:03
0:07:03
 0:34:41
0:34:41
 0:52:01
0:52:01
 1:15:02
1:15:02
 0:00:07
0:00:07
 1:12:48
1:12:48
 0:38:57
0:38:57
 2:20:22
2:20:22
 0:03:26
0:03:26
 0:26:53
0:26:53
 0:50:16
0:50:16
 0:23:03
0:23:03
 0:04:50
0:04:50
 0:58:21
0:58:21
 0:48:53
0:48:53
 0:00:42
0:00:42
 0:15:20
0:15:20
 0:03:18
0:03:18