filmov
tv
Finding Square Root, √ , Without a Calculator

Показать описание
How To Calculate Square Roots - Numerals That Changed Math Forever
Calculating Square Root by Hand (Early Grades)
Find Square Root by Hand without Calculator
How To Find The Square Root of Large Numbers Mentally
Square root in 3 seconds - math trick
What are Square Roots? | Math with Mr. J
How to Approximate Square Root of a Number
Square Root Math Hack
Nice Square Root Math Simplification | Find the Value of X
Math Antics - Exponents and Square Roots
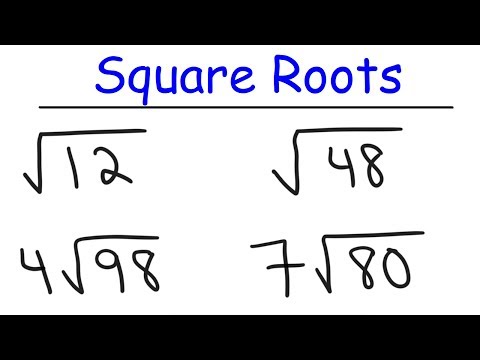
How To Simplify Square Roots
Square root of ANY NUMBER using long division method !👍😊
Square root of ANY number instantly - shortcut math.
How To Find The Square Root of Large Numbers Using The Division Method
How does a calculator find square roots?
How to find Square Root of Perfect Square Number? | Best Square Root Tricks | Math Tricks | Letstute
Do you remember the square roots of these perfect squares? 🤯 #Shorts #math #maths #mathematics
How to Calculate Square Root Without Calculator
How to Manually Compute Square Root of a Large Number (No calculator)
Short Tricks on Square Root in 5 Seconds #shorttricks #shorttricksmaths #shorts
Finding Square root by division method
How to find a square root
Square Roots and Cube Roots | Math with Mr. J
Square root trick! Long division method
Комментарии
 0:10:16
0:10:16
 0:07:24
0:07:24
 0:09:30
0:09:30
 0:12:37
0:12:37
 0:09:46
0:09:46
 0:04:00
0:04:00
 0:00:52
0:00:52
 0:00:23
0:00:23
 0:04:27
0:04:27
 0:11:09
0:11:09
 0:10:46
0:10:46
 0:01:00
0:01:00
 0:08:02
0:08:02
 0:13:54
0:13:54
 0:11:24
0:11:24
 0:04:57
0:04:57
 0:00:11
0:00:11
 0:05:48
0:05:48
 0:07:29
0:07:29
 0:00:45
0:00:45
 0:11:17
0:11:17
 0:05:39
0:05:39
 0:05:03
0:05:03
 0:01:00
0:01:00