filmov
tv
Epicycles, complex Fourier series and Homer Simpson's orbit

Показать описание
NEW (Christmas 2019). Two ways to support Mathologer
(see the Patreon page for details)
Today’s video was motivated by an amazing animation of a picture of Homer Simpson being drawn using epicycles. This video is about making sense of the mathematics epicycles. Highlights include the surprising shape of the Moon’s orbit around the Sun, instructions on how you can make your own epicycle drawings, and a crash course of complex Fourier series to make sense of it all.
In the video I attribute the animation to Santiago which is a mistake. Also Ramiro told me that unlike what it said in "Ptolemy and Homer" their animation actually involved 10000 and not just 1000 epicycles.
Anderstood’s discussion of how to create epicycle drawings in Mathematica lives here:
As usual thank you very much to Danil and Marty for their help with this video.
Enjoy!
(see the Patreon page for details)
Today’s video was motivated by an amazing animation of a picture of Homer Simpson being drawn using epicycles. This video is about making sense of the mathematics epicycles. Highlights include the surprising shape of the Moon’s orbit around the Sun, instructions on how you can make your own epicycle drawings, and a crash course of complex Fourier series to make sense of it all.
In the video I attribute the animation to Santiago which is a mistake. Also Ramiro told me that unlike what it said in "Ptolemy and Homer" their animation actually involved 10000 and not just 1000 epicycles.
Anderstood’s discussion of how to create epicycle drawings in Mathematica lives here:
As usual thank you very much to Danil and Marty for their help with this video.
Enjoy!
Epicycles, complex Fourier series and Homer Simpson's orbit
But what is a Fourier series? From heat flow to drawing with circles | DE4
Python Animation of Fourier Series with Epicycles
Epicycles using Fourier Transform in Polar Coordinates
Fourier Transform and Epicycles
Hilbert curve approximation using epicycles/complex Fourier series
What is a fourier series | drawing with fourier series | epicycles fourier series | transform
Fourier Transformation: Epicycles
Epicycles using Fourier Transformation
Don't Fear Fourier: Epicycles, Complex Numbers and Beyond
One-line Fish epicycles with Fourier Transform
What is a Fourier Series? (Explained by drawing circles) - Smarter Every Day 205
Fourier Transforms - Epicycles and Communism
Fourier Epicycles With Manim #manim#fourierseries #du #msc #advancemath #manimtutorial #animation
Epicycles ¦ Fourier Transformation
Pure Fourier series animation montage
Complex Fourier Series - Epicycles
Writing with Fourier Transform Epicycles
Coding Challenge #130.1: Drawing with Fourier Transform and Epicycles
CT Fourier Series | Complex Signals (Epicycles) #1
Epicycles Using Fourier Transform
Epicycle ¦ Fourier Transformation
SMARTER EVERY DAY Epicycles Fourier Series Drawing
3D Articulated Arms - Epicycles - Polygonal Paths - Fourier Decomposition
Комментарии
 0:25:35
0:25:35
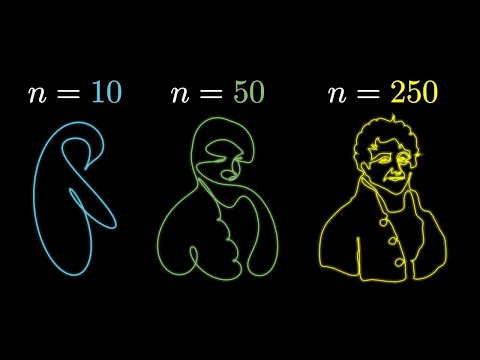 0:24:47
0:24:47
 0:00:20
0:00:20
 0:00:42
0:00:42
 0:00:24
0:00:24
 0:01:54
0:01:54
 0:01:09
0:01:09
 0:00:24
0:00:24
 0:00:42
0:00:42
 0:22:50
0:22:50
 0:00:23
0:00:23
 0:08:25
0:08:25
 0:00:14
0:00:14
 0:01:00
0:01:00
 0:00:37
0:00:37
 0:12:29
0:12:29
 0:08:23
0:08:23
 0:01:35
0:01:35
 0:46:09
0:46:09
 0:02:29
0:02:29
 0:00:27
0:00:27
 0:01:21
0:01:21
 0:02:01
0:02:01
 0:01:52
0:01:52