filmov
tv
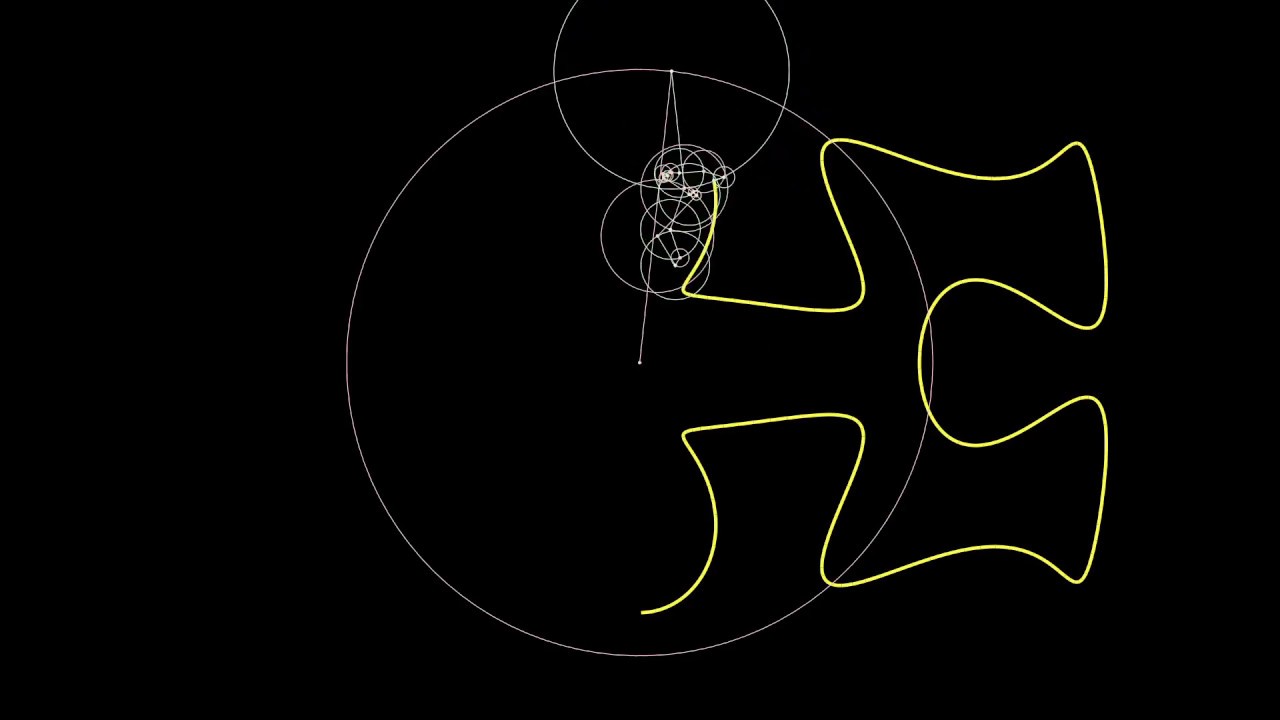
Hilbert curve approximation using epicycles/complex Fourier series
Показать описание
The video linked above also does a great job at explaining the mathematics required into make this video.
In the first section of the video the red lines/circles represent all counter-clockwise rotating epicycles (or exponents of the Fourier series with positive integers) and the green lines/circles represent all clockwise rotating epicycles (or exponents of the Fourier series with negative integers).
In the second section of the video the curves of an increasing order Fourier series are interpolated. This order will jump frequently because due to the symmetry of the Hilbert curve all the even integer Fourier coefficients are zero, so are skipped in the interpolation.
0:01:54
Hilbert curve approximation using epicycles/complex Fourier series
0:06:08
Space-Filling Curves (2 of 4: Hilbert Curve)
0:00:42
Epicycles using Fourier Transform in Polar Coordinates
0:00:16
Hilbert's curve slowly eating the square
0:00:13
Picture to line with Hilbert Curve
0:00:42
Epicycles using Fourier Transformation
0:00:45
Hilbert Curve
0:00:20
Animated L-Systems: Hilbert Curve
0:00:34
Scale invariance of the Hilbert curve
0:00:52
Hilbert Curve 4-EDO Space Filler
0:00:44
Hilbert curve 3D (L-system in TouchDesigner)
0:00:24
Fourier Transform and Epicycles
0:05:27
Hilbert Curve in Processing
0:28:08
Coding the Hilbert Curve
0:00:20
Python Animation of Fourier Series with Epicycles
0:00:21
Visualisation of different approximation of Fourier series
0:00:30
Hilbert Curve Vortex - Draft
0:00:18
Hilbert Curve & back again
0:00:24
Fourier Transformation: Epicycles
0:00:31
Animation of 3D Hilbert Curve (n=3)
0:05:34
Yin-Yang outline drawn by Fourier Series epicycles with zoom ins
0:04:31
Hilbert Curve
0:09:05
Space-Filling Curves (1 of 4: Peano Curve)
0:05:53
Hilbert Curve Cat
Комментарии