filmov
tv
Generating Functions of (Eventually) Constant Sequences

Показать описание
We find the (ordinary) generating function for constant sequences, and for sequences which are eventually constant (i.e. every term is = c after a certain point). After finding the generating function, we explore how our expression is connected to a more general result for non-constant sequences.
More on generating functions:
00:00 Generating functions
00:40 (i) Constant sequences
01:34 (ii) (a, c, c, c, ...)
02:46 (iii) Eventually constant sequences
06:36 Bigger picture
More on generating functions:
00:00 Generating functions
00:40 (i) Constant sequences
01:34 (ii) (a, c, c, c, ...)
02:46 (iii) Eventually constant sequences
06:36 Bigger picture
Generating Functions of (Eventually) Constant Sequences
Generating Functions -- Number Theory 29
A brief introduction to generating functions
Using moment generating functions to generate moments
Counting with Calculus: The Magic of Generating Functions
Generating Functions Part 1: Motivation
Solving Recurrences via Generating Functions. MATH 222, Discrete and Combinatorial Math, UVic
2(d). Multivariate Generating Functions
How to Encode any Sequence into a Function (Generating Functions)
Probability: moment generating functions
Olympiad level counting (Generating functions)
Moment generating function definition
lecture17 Generating functions
SH201A: Probability Theory | Lecture 9 | Generating Functions
[Topics in Combinatorics] Lecture 3. Generating functions
Probability Generating Function #1 properties
UCLA Stats100B Mathematical Statistics: sum of random variable & moment generating functions
Chapter 1b: Ordinary Generating Functions
Moment Generating Functions (II)
Generating Function of sequence part 2
Edexcel A Level Further Maths Further Statistics 1 | Probability Generating Functions
Moment Generating Functions (I)
(PS20) Moment Generating Functions
Properties of Expectations,Variance and Moment Generating Function
Комментарии
 0:09:58
0:09:58
 0:24:41
0:24:41
 0:07:01
0:07:01
 0:02:51
0:02:51
 0:21:52
0:21:52
 0:27:51
0:27:51
 0:23:21
0:23:21
 0:27:30
0:27:30
 0:15:04
0:15:04
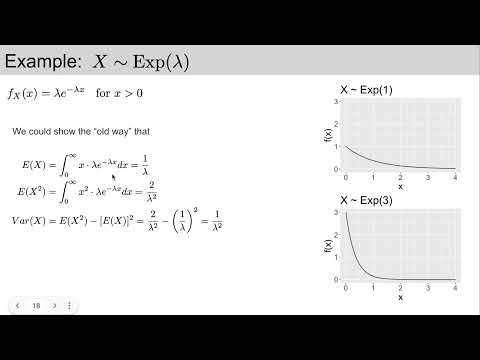 0:14:58
0:14:58
 0:34:36
0:34:36
 0:01:47
0:01:47
 1:26:40
1:26:40
 0:15:49
0:15:49
![[Topics in Combinatorics]](https://i.ytimg.com/vi/pm8J9_QvkaQ/hqdefault.jpg) 1:11:59
1:11:59
 0:10:58
0:10:58
 0:21:47
0:21:47
 1:22:32
1:22:32
 0:18:22
0:18:22
 0:35:30
0:35:30
 0:26:55
0:26:55
 0:16:40
0:16:40
 0:36:28
0:36:28
 0:39:26
0:39:26