filmov
tv
How to Encode any Sequence into a Function (Generating Functions)
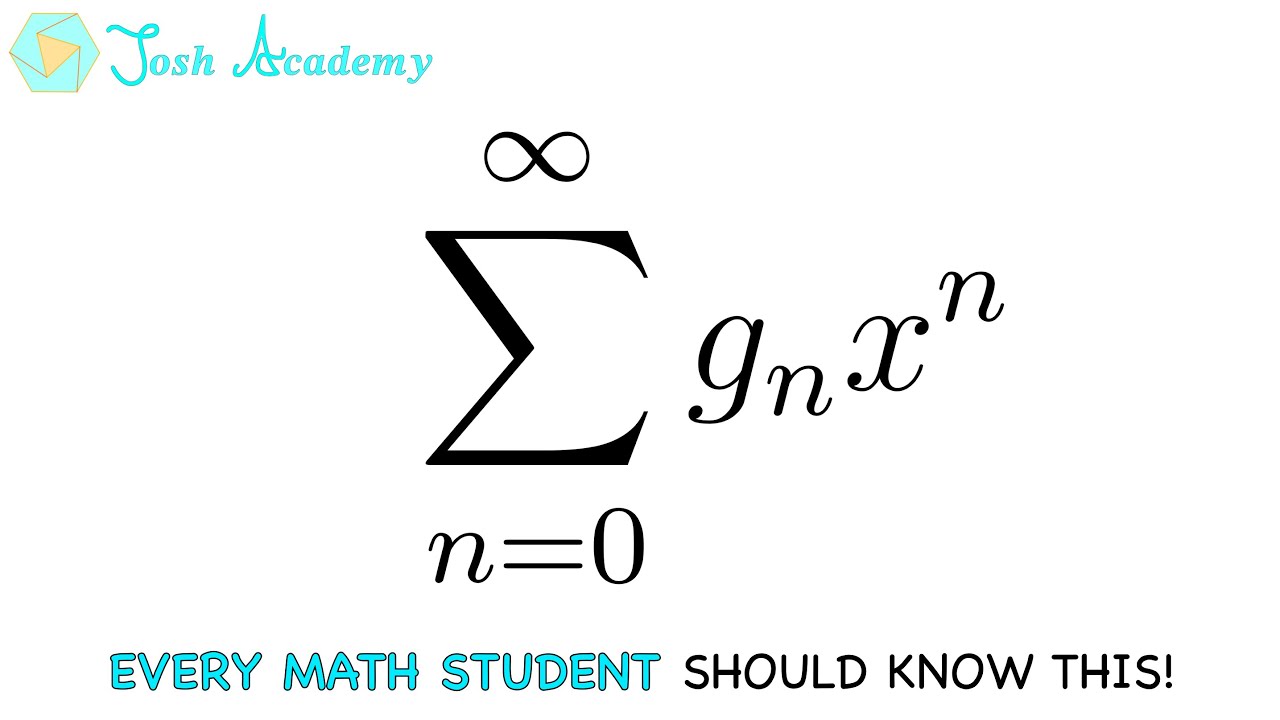
Показать описание
In the previous video of the miniseries, we looked at the Geometric Series as a gateway to understanding Generating Functions and Taylor Series. In this video, we examine properties of Generating Functions and experiment with them by encoding random sequences and looking for nicer expressions.
Apologies for the finicky screen in some parts of the video!
Apologies for the finicky screen in some parts of the video!
How to encode a given String into a sequence or Array of bytes using the getBytes() method
Excel Tip: Sort names alphabetically
Auto Fill Dates in #excel #shorts
Convert date into month text formula #shorts #excel #exceltips
Set a Hanging Indent in Microsoft Word… EASIEST Trick!
Convert Date into a Month TEXT Formula
Excel Tip: Sort Grades Largest to Smallest
How To Resize Videos Like A Pro In Premiere Pro #shorts
Easy LLM Part-1: Interactive Transformer Embeddings & Positional Encoding!
Excel how to change date format in In easy way #Excel #Formulas ✅ (Shortcut # 35 )
Convert Text to Number in Excel - part 2| Excel Tips and tricks | #shorts
Japanese Method #shorts #fyp
Transcription and Translation: From DNA to Protein
Convert DNA to Protein and Protein to DNA sequence | DNA Translation | Expasy | Reverse Translation
Get rid of Scientific Notation and display Numbers in proper format in Excel
How to CONVERT PHOTOS to PDF on iPhone #apple #iphone #tips #tricks #technology
How to convert from one unit to another?
Convert String into Binary Sequence | GeeksforGeeks
Convert photos into pdf file using iPhone #ios #pdf #scanner #tricks #iphone #ipad #techsimplified4u
Convert Data Into table | shortcut to make table in ms word | ms word tips and tricks
How To Convert Gray Code to Binary and Binary to Gray Code
old saree convert into gown with jacket contact no 9990834311#reuseoldsaree #convertoldsaree
BEST METHOD for Installing Recessed Lights!
How to Easily Convert an Image Sequence to a Video in QuickTime on Mac - macOS Monterey | 2022
Комментарии
 0:06:00
0:06:00
 0:00:14
0:00:14
 0:00:11
0:00:11
 0:00:11
0:00:11
 0:00:15
0:00:15
 0:00:25
0:00:25
 0:00:14
0:00:14
 0:00:33
0:00:33
 0:29:04
0:29:04
 0:00:28
0:00:28
 0:00:23
0:00:23
 0:00:20
0:00:20
 0:06:27
0:06:27
 0:04:50
0:04:50
 0:00:49
0:00:49
 0:00:13
0:00:13
 0:00:44
0:00:44
 0:03:33
0:03:33
 0:00:30
0:00:30
 0:00:22
0:00:22
 0:11:00
0:11:00
 0:00:16
0:00:16
 0:00:54
0:00:54
 0:02:03
0:02:03